题目内容
已知数列{an}满足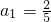 ,且对任意n∈N*,都有2an-2an+1=3anan+1.
,且对任意n∈N*,都有2an-2an+1=3anan+1.
(1)求证:数列 为等差数列;
为等差数列;
(2)试问数列{an}中任意连续两项的乘积ak•ak+1(k∈N*)是否仍是{an}中的项?如果是,请指出是数列的第几项;如果不是,请说明理由.
解:(1)由2an-2an+1=3anan+1,可得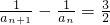 ,(3分)
,(3分)
所以数列 是以
是以 为首项,公差为
为首项,公差为 的等差数列. (6分)
的等差数列. (6分)
(2)由(1)可得数列 的通项公式为
的通项公式为 ,所以
,所以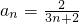 . (8分)
. (8分)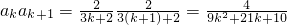
= =
=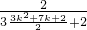 . (10分)
. (10分)
因为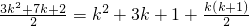 ,(11分)
,(11分)
当k∈N*时, 一定是正整数,所以
一定是正整数,所以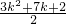 是正整数. (13分)
是正整数. (13分)
所以ak•ak+1是数列{an}中的项,是第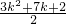 项. (14分)
项. (14分)
分析:(1)直接利用已知条件,通过等差数列的定义,证明数列 为等差数列;
为等差数列;
(2)通过(1)求出数列的通项公式,然后化简ak•ak+1(k∈N*),使得为通项公式的形式,即可判断是否是{an}中的项,然后求是数列的第几项;
点评:本题是中档题,考查等差数列的证明的方法,数列通项公式的应用,考查转化思想、计算能力.
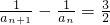 ,(3分)
,(3分)所以数列
 是以
是以 为首项,公差为
为首项,公差为 的等差数列. (6分)
的等差数列. (6分)(2)由(1)可得数列
 的通项公式为
的通项公式为 ,所以
,所以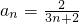 . (8分)
. (8分)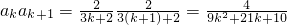
=
 =
=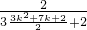 . (10分)
. (10分)因为
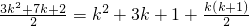 ,(11分)
,(11分)当k∈N*时,
 一定是正整数,所以
一定是正整数,所以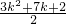 是正整数. (13分)
是正整数. (13分)所以ak•ak+1是数列{an}中的项,是第
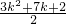 项. (14分)
项. (14分)分析:(1)直接利用已知条件,通过等差数列的定义,证明数列
 为等差数列;
为等差数列;(2)通过(1)求出数列的通项公式,然后化简ak•ak+1(k∈N*),使得为通项公式的形式,即可判断是否是{an}中的项,然后求是数列的第几项;
点评:本题是中档题,考查等差数列的证明的方法,数列通项公式的应用,考查转化思想、计算能力.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目