Question

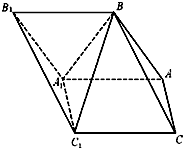已知斜三棱柱ABC-A₁B₁C₁的侧面AA₁C₁C是面积为

3

2

的菱形，∠AA₁C₁为锐角，侧面ABB₁A₁⊥AA₁C₁C，且A₁B=AB=AC=1．
（Ⅰ）求证：AA₁⊥BC₁；
（Ⅱ）求A₁到平面ABC的距离；
（Ⅲ）求二面角B-AC-C₁的余弦值．

Answer 1

分析：（Ⅰ）要证：AA₁⊥BC₁，先说明△AA₁B是等边三角形，设D是AA₁的中点、连接BD，C₁D，证明AA₁⊥平面BC₁D，即可．
（Ⅱ）根据上一问得到的结论，OA、OC₁、OB两两垂直以O为原点，建立如图空间直角坐标系，写出要用的点的坐标，和向量的坐标，根据点到平面的距离公式得到结果．
（Ⅲ）根据上一问做出的平面的法向量，和另一个平面的在图形中存在的法向量，用两个法向量所成的角，得到两个平面之间的夹角的余弦．

解答：解：（Ⅰ）证明：因为四边形AA₁C₁C是菱形，所以有AA₁=A₁C₁=C₁C=CA=1．
从而知△AA₁B是等边三角形．（2分）
设D是AA₁的中点、连接BD，C₁D，
则BD⊥AA₁，由 S菱形A A1C1C =

3

2

．
知C₁到AA₁的距离为

3

2

．∠AA₁C₁=60°，
所以△AA₁C₁是等边三角形，（4分）
且C₁D⊥AA₁，所以AA₁⊥平面BC₁D．（6分）
又BC₁?平面BC₁D，故AA₁⊥BC₁．（7分）

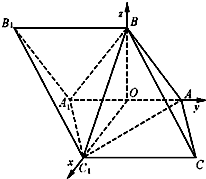
（Ⅱ）由（Ⅰ）知C₁O⊥AA₁，BO⊥AA₁
∵平面ABB₁A₁⊥平面AA₁C₁C，
∴BO⊥平面AA₁C₁C，C₁O?平面AA₁C₁C
BO⊥C₁O
∴OA、OC₁、OB两两垂直，…（6分）
以O为原点，建立如图空间直角坐标系，则：
O（0，0，0），A（0，

1

2

，0），A₁（0，-

1

2

，0），B（0，0，

3

2

），C1(

3

2

，0，0)．…（7分）
设

n

=(x，y．z)
是平面ABC的一个法向量，
则-

1

2

y+

3

2

z=0，

3

2

x+

1

2

y=0
令z=1，则

n

=(-1，

3

，1)．    …（9分）
设A1到平面ABC的距离为d．

AA1

=(0，-1，0)，
∴d=

| AA1 • n  |

| n |

=

15

5

．     …（10分）
（Ⅲ）由（Ⅱ）知平面ABC的一个法向量是

n

=(-1，

3

，1)．，…（11分）
又平面ACC₁的一个法向量

OB

=（0，0，

3

2

）．          …（12分）
∴cosθ=

OB • n

| OB || n |

=

3 2

5 × 3 2

=

5

5

．          …（13分）
∴二面角B-AC-C₁的余弦值是

5

5

．               …（14分）

点评：本题考查直线与平面的垂直，考查空间想象能力，逻辑思维能力，考查用空间向量来解决立体几何距离和面面之间的夹角的问题，是中档题．