题目内容
3．在平面直角坐标系xOy中，A（4，0），B（2，4），C（0，2），动点M在△ABC区域内（含边界）运动，设$\overrightarrow{OM}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OC}$，则λ+μ的取值范围是[1，$\frac{5}{2}$]．分析 作图并设M（x，y），从而由向量可得（x，y）=λ（4，0）+μ（0，2）；从而求得λ+μ=$\frac{x}{4}$+$\frac{y}{2}$，从而转化为线性规划问题求解即可．
解答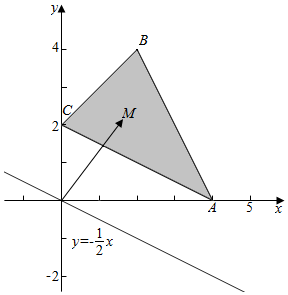 
解：如图，设M（x，y），
所以（x，y）=λ（4，0）+μ（0，2）；
故λ=$\frac{x}{4}$，μ=$\frac{y}{2}$，所以λ+μ=$\frac{x}{4}$+$\frac{y}{2}$，
问题等价于当M在△ABC内（含边界）运动时，
求z=$\frac{x}{4}$+$\frac{y}{2}$的取值范围，
运用线性规划知识可知
当M在点B时zmax=$\frac{5}{2}$，当M在AC上任意一点时zmin=1，
所以λ+μ取值范围是[1，$\frac{5}{2}$]．
故答案为：[1，$\frac{5}{2}$]．
点评 本题考查了线性规划的变形应用及平面向量的应用，同时考查了数形结合的思想方法应用，属于中档题．
练习册系列答案
相关题目
18．某企业A向杜会迸行融资，先让个人B借给企业a万元（a＞0），再从出借日的下个月开始，分成12个月，按月复利1%计算，每月企业等额返还给个人B，现企业A前6个月已按约定返还给个人B，由于某种特殊原因该融资必须停止，企业退还给B $\frac{a}{2}$万元，则该退还方式（ ）
| A． | 公平 | B． | 企业A吃亏 | C． | 个人B吃亏 | D． | 谁吃亏与a有关 |
8．若5人站一排，且甲、乙之间至多有一个人，这样的站法有（ ）种．
| A． | 84 | B． | 60 | C． | 144 | D． | 76 |
15．已知平面向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$满足$\overrightarrow{a}$$•\overrightarrow{a}$=$\overrightarrow{a}$$•\overrightarrow{b}$=$\overrightarrow{b}$$•\overrightarrow{c}$=1，$\overrightarrow{a}$$•\overrightarrow{c}$=2，则|$\overrightarrow{a}$$+\overrightarrow{b}$$+\overrightarrow{c}$|的取值范围为（ ）
| A． | [0，+∞） | B． | [2$\sqrt{2}$，+∞） | C． | [2$\sqrt{3}$，+∞） | D． | [4，+∞） |
12．若函数f（x）=sin（ωx+φ），其中$ω＞0，|φ|＜\frac{π}{2}，x∈R$，两相邻对称轴的距离为$\frac{π}{2}$，$f（{\frac{π}{6}}）$为最大值，则函数f（x）在区间[0，π]上的单调增区间为（ ）
| A． | $[{0，\frac{π}{6}}]$ | B． | $[{\frac{2π}{3}，π}]$ | C． | $[{0，\frac{π}{6}}]$和$[{\frac{π}{3}，π}]$ | D． | $[{0，\frac{π}{6}}]$和$[{\frac{2π}{3}，π}]$ |