题目内容
若定义在R上的函数 满足:
满足: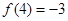 ,且对任意
,且对任意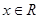 满足
满足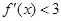 ,
,
则不等式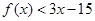 的解集为( ).
的解集为( ).
A.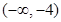 | B.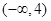 | C.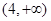 | D.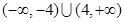 |
C
解析试题分析:构造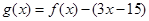 ,则
,则 ;因为对任意
;因为对任意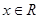 满足
满足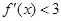 ,所以
,所以 恒成立,即
恒成立,即 在
在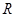 上为减函数;又因为
上为减函数;又因为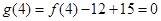 ,所以
,所以 的解集为
的解集为 .
.
考点:抽象不等式的解集.

练习册系列答案
 能力评价系列答案
能力评价系列答案
相关题目
函数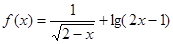 的定义域为
的定义域为
A. | B.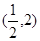 | C.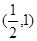 | D.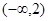 |
函数 的值域是( )
的值域是( )
| A.(0,+∞) | B.(0,1) | C.(0,1] | D.[1,+∞) |
下列函数中,满足“ ”的单调递增函数是( )
”的单调递增函数是( )
A. | B.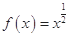 | C.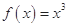 | D.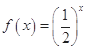 |
函数 的图像( ).
的图像( ).
| A.关于原点对称 | B.关于主线 对称 对称 |
C.关于 轴对称 轴对称 | D.关于直线 对称 对称 |
下列函数中,与函数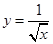 有相同定义域的是( ).
有相同定义域的是( ).
A.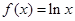 | B.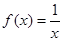 | C.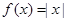 | D.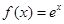 |
已知函数 则实数
则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
设奇函数 在
在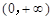 上为增函数,且
上为增函数,且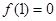 ,则不等式
,则不等式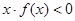 的解集为( )
的解集为( )
A. | B.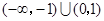 |
C. | D.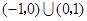 |
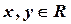 ,求证:
,求证: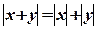 成立的充要条件是xy≥0.(8分)
成立的充要条件是xy≥0.(8分)