题目内容
(14分)已知在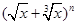 (其中n<15)的展开式中:
(其中n<15)的展开式中:
(1)求二项式展开式中各项系数之和;
(2)若展开式中第9项,第10项,第11项的二项式系数成等差数列,求n的值;
(3)在(2)的条件下写出它展开式中的有理项.
(1) ; (2)n=14; (3)
; (2)n=14; (3) ,
, ,
, .
.
解析试题分析:(1)二项展开式中各项的系数和就是 ,由
,由 可得结果;(2)由二项式系数
可得结果;(2)由二项式系数 ,
, ,
, 成等差数列,
成等差数列, ,解得n="14;" (3)
,解得n="14;" (3) 可知,有理项中知
可知,有理项中知 应该是6的倍数.
应该是6的倍数.
解:(1)因为本题二项展开式中各项的系数就是各项的二项式系数
所以各项系数之和为 4分
4分
(2)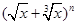 (其中n<15)的展开式中第9项,第10项,第11项的二项式系数
(其中n<15)的展开式中第9项,第10项,第11项的二项式系数
分别是 ,
, ,
, .-----------6分
.-----------6分
依题意得 ,写成:
,写成: , 7分
, 7分
化简得90+(n-9)(n-8)=2·10(n-8),
即:n2-37n+322=0,解得n=14或n=23,因为n<15所以n=14。 9分
(2)展开式的通项  11分
11分
展开式中的有理项当且仅当r是6的倍数, 12分
0≤r≤14,所以展开式中的有理项共3项是: ;
; ;
; 14分
14分
考点:1.二项式定理;2.等差数列.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 ,则
,则 ______.(用数字作答)
______.(用数字作答)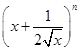 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列. 的展开式中,第6项
的展开式中,第6项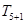 为常数项.
为常数项. 的展开式中,
的展开式中,  的一次项系数是
的一次项系数是 ,则实数
,则实数 的值为
的值为 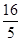 x2+
x2+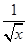 )5的展开式的常数项,而(a2+1)n的展开式的二项式系数最大的项等于54,求a的值.
)5的展开式的常数项,而(a2+1)n的展开式的二项式系数最大的项等于54,求a的值. -
- )n的展开式中,第五项与第三项的二项式系数之比为14∶3,求展开式中的常数项.
)n的展开式中,第五项与第三项的二项式系数之比为14∶3,求展开式中的常数项.