Question

 

某企业拟建造如图所示的容器（不计厚度，长度单位：米），其中容器的中间为圆柱形，左右两端均为半球形，按照设计要求容器的体积为立方米，且.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元，半球形部分每平方米建造费用为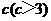千元.设该容器的建造费用为千元.

（Ⅰ）写出关于的函数表达式，并求该函数的定义域；

（Ⅱ）求该容器的建造费用最小时的.

 

 

Answer 1

【答案】

 

【解析】（Ⅰ）因为容器的体积为立方米，

所以,

解得,

由于

因此。

所以圆柱的侧面积为=,

两端两个半球的表面积之和为,

所以建造费用+,定义域为.

 （Ⅱ）因为+=,

由于c>3,所以c-2>0,

所以令得: ;

令得:,

（1）   当时，即时，函数y在（0，2）上是单调递减的，故建造费最小时r=2。

（2）   当时，即时，函数y在（0，2）上是先减后增的，故建造费最小时。