题目内容
已知函数f(x)=2ax+ 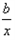 +lnx,
+lnx,
(1)若函数f(x)在x=1,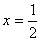 处取得极值,求a,b的值;
处取得极值,求a,b的值;
(2)若f′(1)=2,函数f(x)在(0,+∞)上是单调函数,求a的取值范围。
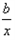 +lnx,
+lnx,(1)若函数f(x)在x=1,
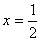 处取得极值,求a,b的值;
处取得极值,求a,b的值;(2)若f′(1)=2,函数f(x)在(0,+∞)上是单调函数,求a的取值范围。
解:(1)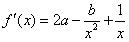 ,
,
由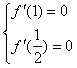 ,可得
,可得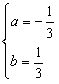 ;
;
(2)函数f(x)的定义域是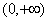 ,
,
因为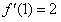 ,
,
所以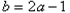 ,
,
所以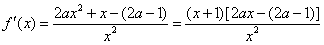 ,
,
要使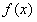 在
在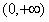 上是单调函数,
上是单调函数,
只要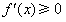 或
或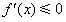 在
在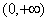 上恒成立;
上恒成立;
当 时,
时,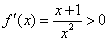 恒成立,
恒成立,
所以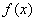 在
在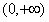 上是单调函数;
上是单调函数;
当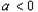 时,令
时,令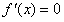 ,得
,得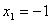 ,
,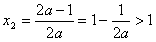 ,
,
此时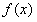 在
在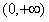 上不是单调函数;
上不是单调函数;
当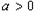 时,要使
时,要使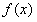 在
在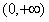 上是单调函数,
上是单调函数,
只要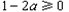 ,即
,即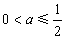 ;
;
综上所述,a的取值范围是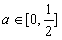 。
。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目