题目内容
设90°<α<180°,角α的终边上一点为P(x,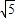 ),且cosα=
),且cosα=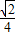 x,求sinα与tanα的值.
x,求sinα与tanα的值.
【答案】分析:先根据条件判断 x<0,由余弦函数的定义求得x值,根据sinα、tanα 的定义求出它们的值.
解答:解:∵90°<α<180°,角α的终边上一点为P(x, ),且cosα=
),且cosα= x,∴x<0,
x,∴x<0,
∴OP=r= ,cosα=
,cosα= x=
x= =
= ,解得 x=-
,解得 x=- .∴OP=2
.∴OP=2 ,
,
∴sinα= =
= =
= ,tanα=
,tanα= =
= =-
=- .
.
点评:本题考查任意角的三角函数的定义,两点间的距离公式的应用,求出x 值,是解题的关键.
解答:解:∵90°<α<180°,角α的终边上一点为P(x,
 ),且cosα=
),且cosα= x,∴x<0,
x,∴x<0,∴OP=r=
 ,cosα=
,cosα= x=
x= =
= ,解得 x=-
,解得 x=- .∴OP=2
.∴OP=2 ,
,∴sinα=
 =
= =
= ,tanα=
,tanα= =
= =-
=- .
.点评:本题考查任意角的三角函数的定义,两点间的距离公式的应用,求出x 值,是解题的关键.

练习册系列答案
相关题目
 ,则
,则 的值为 .
的值为 .
 )的值为( )
)的值为( )




 ,则
,则 的值为 .
的值为 .
 ),且cosα=
),且cosα= x,求sinα与tanα的值;
x,求sinα与tanα的值;