题目内容
已知函数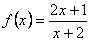 ,试证明f(x)在(-2,+∞)上是单调增函数,并求该函数在区间[1,4]上的最大值、最小值。
,试证明f(x)在(-2,+∞)上是单调增函数,并求该函数在区间[1,4]上的最大值、最小值。
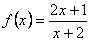 ,试证明f(x)在(-2,+∞)上是单调增函数,并求该函数在区间[1,4]上的最大值、最小值。
,试证明f(x)在(-2,+∞)上是单调增函数,并求该函数在区间[1,4]上的最大值、最小值。 解:设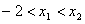 ,则
,则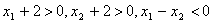 ,
,
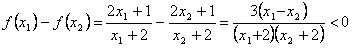 ,
,
所以f(x) 在(-2,+∞)上单调递增;
由上可知f(x)在[1,4]上单调递增,
所以f(x)的最小值为f(1)=1,f(x)的最大值为f(4)=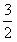 。
。
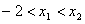 ,则
,则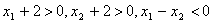 ,
,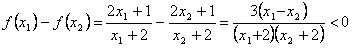 ,
,所以f(x) 在(-2,+∞)上单调递增;
由上可知f(x)在[1,4]上单调递增,
所以f(x)的最小值为f(1)=1,f(x)的最大值为f(4)=
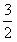 。
。 
练习册系列答案
相关题目
 ,试证明f(x)在区间(-2,+∞)上是增函数,并求出该函数在区间[1,4]上的最大值和最小值.
,试证明f(x)在区间(-2,+∞)上是增函数,并求出该函数在区间[1,4]上的最大值和最小值.