题目内容
己知
=(-1,x2+m),
=(m+1,
),当m>0时,求使不等式
•
>0成立的x的取值范围.
| a |
| b |
| 1 |
| x |
| a |
| b |
分析:由题意,先利用数量积公式将不等式变为
>0,再讨论m的取值范围,解不等式得出x的取值范围
| (x-1)(x-m) |
| x |
解答:解:∵
•
=-(m+1)+
=
=
>0
∴当m>l时,如下图(1),可得,使不等式成立的x∈(0,1)∪(m,+∞)•
当m=l时,如下图(2),可得,使不等式成立的x∈(0,1)∪(1,+∞);
当0<m<l时,如下图(3),可得,使不等式成立的x∈(0,m)∪(1,+∞);
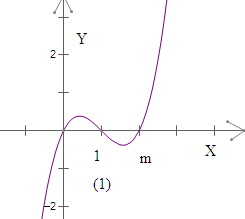
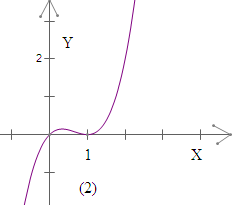
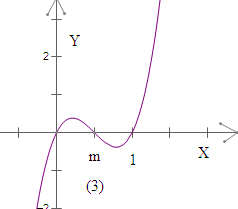
| a |
| b |
| x2+m |
| x |
| x2-(m+1)x+m |
| x |
| (x-1)(x-m) |
| x |
∴当m>l时,如下图(1),可得,使不等式成立的x∈(0,1)∪(m,+∞)•
当m=l时,如下图(2),可得,使不等式成立的x∈(0,1)∪(1,+∞);
当0<m<l时,如下图(3),可得,使不等式成立的x∈(0,m)∪(1,+∞);
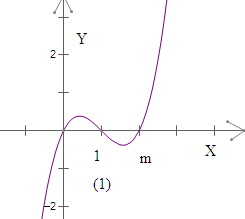
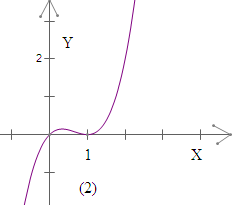
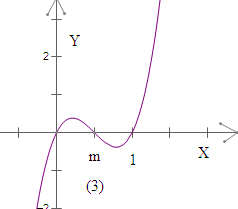
点评:本题中考查平面向量数量积的运算,不等式的解法,解题的关键是熟练掌握数量积公式及代数法解不等式,本题考查了利用公式计算的能力及分类讨论的思想,数形结合的思想

练习册系列答案
相关题目
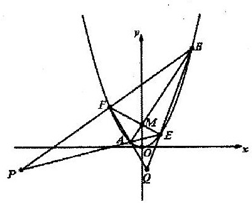 (2012•浙江模拟)己知抛物线C:x2=2py(p>0)上一点T(m,4)到其焦点的距离为
(2012•浙江模拟)己知抛物线C:x2=2py(p>0)上一点T(m,4)到其焦点的距离为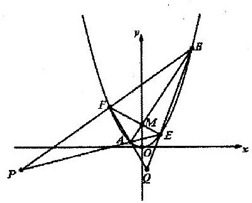 己知抛物线C:x2=2py(p>0)上一点T(m,4)到其焦点的距离为
己知抛物线C:x2=2py(p>0)上一点T(m,4)到其焦点的距离为 .
.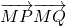 是定值.
是定值.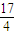 .
.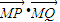 是定值.
是定值.