Question

已知椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0）的右准线l的方程为x=

4 3

3

，短轴长为2．
（1）求椭圆C的方程；
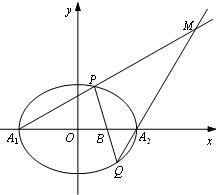
（2）过定点B（1，0）作直线l与椭圆C相交于P，Q（异于A₁，A₂）两点，设直线PA₁与直线QA₂相交于点M（2x₀，y₀）．
①试用x₀，y₀表示点P，Q的坐标；
②求证：点M始终在一条定直线上．

Answer 1

分析：（1）由题设条件能够得到

a2=4 b2=1.

，由此可求出椭圆C的方程．
（2）A₁（-2，0），A₂（2，0），方程为MA₁的方程为：y=

y0

2x0+2

(x+2)，代入

x2

4

+y2=1，
得[

(x0+1)2

y02

+1] y2-

2(x0+1)

y0

y=0．P（

4(x0+1)2

(x0+1)2+y02

-2，

2(x0+1)y0

(x0+1)2+y02

）．同理可得Q（

-4(x0-1)2

(x0-1)2+y02

+2，

-2(x0-1)y0

(x0-1)2+y02

）．再由P，Q，B三点共线，知k_PB=k_QB，从而得到点M始终在定直线x=4上．

解答：解：（1）由

a2 c = 4 3 3 b=1 a2=b2+c2

得

a2=4 b2=1.

∴椭圆C的方程为

x2

4

+y2=1；
（2）A₁（-2，0），A₂（2，0），
方程为MA₁的方程为：y=

y0

2x0+2

(x+2)，即x=

2x0+2

y0

y-2．代入

x2

4

+y2=1，
得(

x0+1

y0

y-1)2+y2=1，即[

(x0+1)2

y02

+1]y2-

2(x0+1)

y0

y=0．
∴yP=

2(x0+1) y0

(x0+1)2 y02 +1

=

2(x0+1)y0

(x0+1)2+y02

，
则xP=

2x0+2

y0

•

2(x0+1)y0

(x0+1)2+y02

-2=

4(x0+1)2

(x0+1)2+y02

-2．
即P（

4(x0+1)2

(x0+1)2+y02

-2，

2(x0+1)y0

(x0+1)2+y02

）．
同理MA₂的方程为y=

y0

2x0-2

(x-2)，即x=

2x0-2

y0

y+2．代入

x2

4

+y2=1，
得(

x0-1

y0

y+1)2+y2=1，即[

(x0-1)2

y02

+1]y2+

2(x0-1)

y0

y=0．
∴yQ=

- 2(x0-1) y0

(x0-1)2 y02 +1

=

-2(x0-1)y0

(x0-1)2+y02

．
则xQ=

2x0-2

y0

•

-2(x0-1)y0

(x0-1)2+y02

+2=

-4(x0-1)2

(x0-1)2+y02

+2．
即Q（

-4(x0-1)2

(x0-1)2+y02

+2，

-2(x0-1)y0

(x0-1)2+y02

）．
∵P，Q，B三点共线，
∴k_PB=k_QB，即

yP

xP-1

=

yQ

xQ-1

．
∴

2(x0+1)y0 (x0+1)2+y02

4(x0+1)2 (x0+1)2+y02 -2-1

=

-2(x0-1)y0 (x0-1)2+y02

-4(x0-1)2 (x0-1)2+y02 +2-1

．
即

(x0+1)y0

(x0+1)2-3y02

=

-(x0-1)y0

-3(x0-1)2+y02

．
由题意，y₀≠0，
∴

x0+1

(x0+1)2-3y02

=

x0-1

3(x0-1)2-y02

．
3（x₀+1）（x₀-1）²-（x₀+1）y₀²=（x₀-1）（x₀+1）²-3（x₀-1）y₀²．
∴（2x₀-4）（x₀²+y₀²-1）=0．则2x₀-4=0或x₀²+y₀²=1．
若x₀²+y₀²=1，即

(2x0)2

4

+y02=1，则P，Q，M为同一点，不合题意．
∴2x₀-4=0，点M始终在定直线x=2上．

点评：本题考查直线和圆锥曲线的综合应用，解题时要认真审题，仔细解答，注意培养计算能力．