题目内容
如图,四边形ABCD与A'ABB'都是边长为a的正方形,点E是A'A的中点,A'A⊥平面ABCD.(I)计算:多面体A'B'BAC的体积;
(II)求证:A'C∥平面BDE;
(Ⅲ)求证:平面A'AC⊥平面BDE.
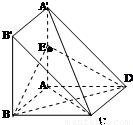
【答案】分析:(I)多面体A'B'BAC是一个以A'B'BA为底,C点为顶点的四棱锥,由图形知其体积易求;
(II)欲证A'C∥平面BDE,只须在面内找到一条线与线A'C平行即可,由图形知,此线为一中位线,易作,易证;
(Ⅲ)欲证平面A'AC⊥平面BDE.先证BD⊥平面A'AC即可.
解答: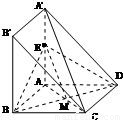 (I)解:多面体A'B'BAC是一个以A'B'BA为底,C点为顶点的四棱锥,由已知条件,知BC⊥平面A'B'BA,
(I)解:多面体A'B'BAC是一个以A'B'BA为底,C点为顶点的四棱锥,由已知条件,知BC⊥平面A'B'BA,
∴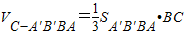
=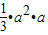
=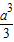 (3分)
(3分)
(II)证:设AC交BD于M,连接ME.
∵ABCD为正方形,所以M为AC中点,
又∵E为A'A的中点
∴ME为△A'AC的中位线∴ME∥A'C(5分)
∵ME?平面BDE,A'C?平面BDE
∴A'C∥平面BDE.(7分)
(Ⅲ)证:∵ABCD为正方形
∴BD⊥AC(9分)
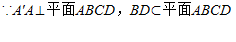
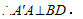
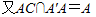
∴BD⊥平面A′AC.(11分)
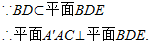 (12分)
(12分)
点评:本题考点是组合体的面积、体积问题,考查了组合体的体积求法以及线面平行,面面垂直的证明,属于直接用定理证明的题型,是立体几何中的基本题型.
(II)欲证A'C∥平面BDE,只须在面内找到一条线与线A'C平行即可,由图形知,此线为一中位线,易作,易证;
(Ⅲ)欲证平面A'AC⊥平面BDE.先证BD⊥平面A'AC即可.
解答:
 (I)解:多面体A'B'BAC是一个以A'B'BA为底,C点为顶点的四棱锥,由已知条件,知BC⊥平面A'B'BA,
(I)解:多面体A'B'BAC是一个以A'B'BA为底,C点为顶点的四棱锥,由已知条件,知BC⊥平面A'B'BA,∴
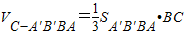
=
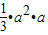
=
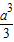 (3分)
(3分)(II)证:设AC交BD于M,连接ME.
∵ABCD为正方形,所以M为AC中点,
又∵E为A'A的中点
∴ME为△A'AC的中位线∴ME∥A'C(5分)
∵ME?平面BDE,A'C?平面BDE
∴A'C∥平面BDE.(7分)
(Ⅲ)证:∵ABCD为正方形
∴BD⊥AC(9分)
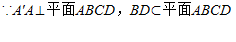
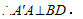
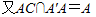
∴BD⊥平面A′AC.(11分)
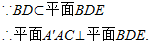 (12分)
(12分)点评:本题考点是组合体的面积、体积问题,考查了组合体的体积求法以及线面平行,面面垂直的证明,属于直接用定理证明的题型,是立体几何中的基本题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,四边形ABCD与A′ABB′都是边长为a的正方形,点E是A′A的中点,A′A⊥平面ABCD.
如图,四边形ABCD与A′ABB′都是边长为a的正方形,点E是A′A的中点,A′A⊥平面ABCD. 如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=
如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB= 如图,四边形ABCD为矩形,且AD=2,AB=1,PA⊥平面ABCD,PA=1,E为BC的中点.
如图,四边形ABCD为矩形,且AD=2,AB=1,PA⊥平面ABCD,PA=1,E为BC的中点. 如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD
如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD
 如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=