Question

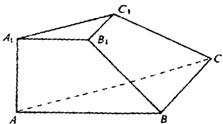如图，在三棱台A₁B₁C₁-ABC中，已知A₁A⊥底面ABC，A₁A=A₁B₁=B₁C₁=a，B₁B⊥BC，且B₁B和底面ABC所成的角45°，求这个棱台的体积．

Answer 1

分析：利用直线和平面垂直的判定定理可以推出BC⊥侧面A₁ABB₁，从而根据平面的垂线的定义又可得出BC⊥AB，∠ABB₁就是BB₁和底面ABC所成的角，求出AB、BC，再利用棱台的体积公式求出体积即可．

解答：解：因为A₁A⊥底面ABC，所以根据平面的垂线的定义有A₁A⊥BC．
又BC⊥BB₁，且棱AA₁和BB₁的延长线交于一点，
所以利用直线和平面垂直的判定定理可以推出BC⊥侧面A₁ABB₁，
从而根据平面的垂线的定义又可得出BC⊥AB．
∴△ABC是直角三角形，∠ABC=90°．
并且∠ABB₁就是BB₁和底面ABC所成的角，
∠ABB₁=45°．
作B₁D⊥AB交AB于D，则B₁D∥A₁A，故B₁D⊥底面ABC．
∵Rt△B₁DB中∠DBB₁=45°，
∴DB=DB₁=AA₁=a，
∴AB=2a．
由于棱台的两个底面相似，故
Rt△ABC∽Rt△A₁B₁C₁．
∵B₁C₁=A₁B₁=a，AB=2a，
∴BC=2a．
∴S_上=

1

2

A₁B₁×B₁C₁=

a2

2

．
S_下=

1

2

AB×BC=2a²．
V棱台=

1

3

•A₁A•(S上+

S上•S下

+S下)
=

1

3

•a•(

a2

2

+

a2 2 ×2a2

+2a2)=

7

6

a3．

点评：本题主要考查了直线与平面之间的位置关系，考查空间想象能力、运算能力和推理论证能力，属于基础题．