题目内容
已知函数 .若f(x)≥lnx+m-1在[1,+∞)上恒成立,
.若f(x)≥lnx+m-1在[1,+∞)上恒成立,
(1)求m取值范围;
(2)证明:2ln2+3ln3+…+nlnn (n∈N*).
(n∈N*).
解:(1)由题意,令 在x∈[1,+∞)上恒成立
在x∈[1,+∞)上恒成立
 …4分
…4分
当 时,即m≥1时g′(x)≤0在[1,+∞)恒成立,∴g(x)在其上递减.
时,即m≥1时g′(x)≤0在[1,+∞)恒成立,∴g(x)在其上递减.
∵gmax=g(1)≤0
∴原式成立.
当 ,即0<m<1时,∵
,即0<m<1时,∵
∴不能恒成立.
综上:m≥1…9分
(2)证明:取m=1,则lnx ,∴
,∴
令x=n,∴
∴
∵
∴2ln2+3ln3+…+nlnn ,原不等式成立…12分
,原不等式成立…12分
分析:(1)由题意,令 在x∈[1,+∞)上恒成立,求导函数,分类讨论,确定函数的单调性与最值,即可确定m取值范围;
在x∈[1,+∞)上恒成立,求导函数,分类讨论,确定函数的单调性与最值,即可确定m取值范围;
(2)取m=1,则lnx ,令x=n,可得
,令x=n,可得 ,累加并化简可得结论.
,累加并化简可得结论.
点评:本题考查恒成立问题,考查导数知识的运用,考查不等式的证明,正确求导,合理取值是关键.
 在x∈[1,+∞)上恒成立
在x∈[1,+∞)上恒成立 …4分
…4分当
 时,即m≥1时g′(x)≤0在[1,+∞)恒成立,∴g(x)在其上递减.
时,即m≥1时g′(x)≤0在[1,+∞)恒成立,∴g(x)在其上递减.∵gmax=g(1)≤0
∴原式成立.
当
 ,即0<m<1时,∵
,即0<m<1时,∵
∴不能恒成立.
综上:m≥1…9分
(2)证明:取m=1,则lnx
 ,∴
,∴
令x=n,∴

∴

∵

∴2ln2+3ln3+…+nlnn
 ,原不等式成立…12分
,原不等式成立…12分分析:(1)由题意,令
 在x∈[1,+∞)上恒成立,求导函数,分类讨论,确定函数的单调性与最值,即可确定m取值范围;
在x∈[1,+∞)上恒成立,求导函数,分类讨论,确定函数的单调性与最值,即可确定m取值范围;(2)取m=1,则lnx
 ,令x=n,可得
,令x=n,可得 ,累加并化简可得结论.
,累加并化简可得结论.点评:本题考查恒成立问题,考查导数知识的运用,考查不等式的证明,正确求导,合理取值是关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
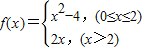 ,若f(x)=12,则x= .
,若f(x)=12,则x= .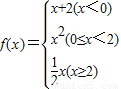 ,若f(x)=2,则x的值为( )
,若f(x)=2,则x的值为( )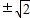
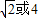
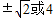
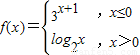 ,若f(x)≥1,则x的取值范围为 .
,若f(x)≥1,则x的取值范围为 .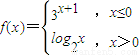 ,若f(x)≥1,则x的取值范围为 .
,若f(x)≥1,则x的取值范围为 .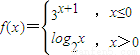 ,若f(x)≥1,则x的取值范围为 .
,若f(x)≥1,则x的取值范围为 .