题目内容
△ABC的内角A,B,C的对边分别为a,b,c,若a2+c2=b2+ac,且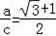 ,求B和C.
,求B和C.
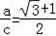 ,求B和C.
,求B和C.解:因为a2+c2=b2+ac得 b2=a2+c2﹣ac,
又因为b2=a2+c2﹣2accosB,
所以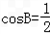 ,
,
所以B=60°
因为由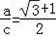 可得
可得 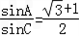 ,
,
所以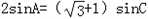
∴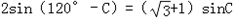 ,得sinC=cosC,
,得sinC=cosC,
所以C=45°
又因为b2=a2+c2﹣2accosB,
所以
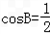 ,
,所以B=60°
因为由
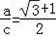 可得
可得 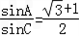 ,
,所以
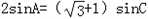
∴
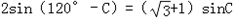 ,得sinC=cosC,
,得sinC=cosC,所以C=45°

练习册系列答案
相关题目