题目内容
【题目】已知抛物线 ![]() :
: ![]() ,
, ![]() 为
为 ![]() 上一点且纵坐标为
上一点且纵坐标为 ![]() ,
, ![]() ,
, ![]() 是
是 ![]() 上的两个动点,且
上的两个动点,且 ![]() .
.
(1)求过点 ![]() ,且与
,且与 ![]() 恰有一个公共点的直线
恰有一个公共点的直线 ![]() 的方程;
的方程;
(2)求证: ![]() 过定点.
过定点.
【答案】
(1)解:由题意得 ![]() ,显然直线
,显然直线 ![]() 符合题意;
符合题意;
当 ![]() 时,设
时,设 ![]() 的方程为
的方程为 ![]() ,由
,由 ![]()
得 ![]() ,令
,令 ![]() ,解得
,解得 ![]() ,
,
于是 ![]() ,所以
,所以 ![]() 的方程为
的方程为 ![]() 或
或 ![]()
(2)解:设 ![]() ,
, ![]() ,于是
,于是 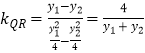 ,
,
于是直线 ![]() 的方程为
的方程为 ![]() ,
,
即 ![]() ①,又
①,又 ![]() ,所以
,所以 ![]() ,
,
易得 ![]() ,
, ![]() ,于是
,于是 ![]() .
.
即 ![]() ,与①联立,消去
,与①联立,消去 ![]() ,
,
得 ![]() ,令
,令 ![]() ,得
,得 ![]() ,故过定点
,故过定点 ![]()
【解析】(1)分情况讨论直线斜率存在和不存在,当斜率不存在时结合题意可得满足。当斜率存在时由直线方程的点斜式设出方程再与抛物线的方程联立,消元得到关于y的方程根据题意直线和抛物线相切进而方程的判别式等于零,即可求出m的值进而得到直线的方程。(2)根据题意分别求出点P、Q的坐标,然后求出直线QR的斜率由直线的点斜式求出直线的方程,整理化简再结合两直线垂直斜率之积等于-1得到关于y1和y2的代数式,利用整体思想结合代数式的几何意义的出x、y的值,进而可得QR过定点。

练习册系列答案
相关题目

