题目内容
设正实数
满足
,则当
取得最大值时,
的最大值为 ( )
| A．0 | B．1 | C． | D．3 |
D
解析试题分析：根据题意，由于正实数满足，当
取得最大值时,x=2y,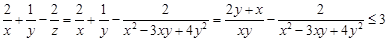
,故可知答案为D.
考点：不等式的运用
点评：主要是考查了均值不等式的运用，属于基础题。
练习册系列答案
中考解读考点精练系列答案
相关题目
若正实数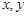
满足
，且
恒成立，则 
的最大值为（ ）
| A．1 | B．2 | C．3 | D．4 |
在如图所示的锐角三角形空地中，欲建一个面积最大的内接矩形花园（阴影部分），则其边长x为 ( )
| A．35m | B．30m | C．25m | D．20m |
已知
，则
的最小值是（ ）
| A．2 | B． | C．4 | D．5 |
若实数
，
满足
，则
的最小值为（ ）
| A．18 | B．12 | C．9 | D．6 |
若一个矩形的对角线长为常数
，则其面积的最大值为 （ ）
A． | B． | C． | D． |
函数y＝
(x>1)的最小值为( )
| A．－4 | B．－3 | C．3 | D．4 |
若
且满足
，则
的最小值是（ ）
A． | B． | C． | D． |
设正实数
满足
，则当
取得最大值时，
的最大值为( )
A． | B． | C． | D． |