题目内容
一个袋子装有大小形状完全相同的9个球,其中5个红球编号分别为1,2,3,4,5,4个白球编号分别为1,2,3,4,从袋中任意取出3个球.
(1)求取出的3个球编号都不相同的概率;
(2)记X为取出的3个球中编号的最小值,求X的分布列与数学期望.
(1)求取出的3个球编号都不相同的概率;
(2)记X为取出的3个球中编号的最小值,求X的分布列与数学期望.
(1) (2)
(2)
 (2)
(2)
记“取出的3个球编号都不相同”为事件A,“取出的3个球中恰有两个球编号相同”为事件B,则P(B)= =
= =
= ,∴P(A)=1-P(B)=
,∴P(A)=1-P(B)= .
.
(2)X的取值为1,2,3,4
P(X=1)= =
= ,P(X=2)=
,P(X=2)= =
= ,
,
P(X=3)= =
= ,P(X=4)=
,P(X=4)= =
= .
.
所以X的分布列为
E(X)=1× +2×
+2× +3×
+3× +4×
+4× =
= =
= .
.
 =
= =
= ,∴P(A)=1-P(B)=
,∴P(A)=1-P(B)= .
.(2)X的取值为1,2,3,4
P(X=1)=
 =
= ,P(X=2)=
,P(X=2)= =
= ,
,P(X=3)=
 =
= ,P(X=4)=
,P(X=4)= =
= .
.所以X的分布列为
| X | 1 | 2 | 3 | 4 |
| P |  |  |  |  |
 +2×
+2× +3×
+3× +4×
+4× =
= =
= .
.
练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
 ,求随机变量
,求随机变量 名网友的网购金额情况,得到如下数据统计表(如图):
名网友的网购金额情况,得到如下数据统计表(如图):

 千元的顾客定义为“网购达人”,网购金额不超过
千元的顾客定义为“网购达人”,网购金额不超过 .
. ,
, ,
, ,
, 的值,并补全频率分布直方图(如图(2)).
的值,并补全频率分布直方图(如图(2)). 名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定
名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定 人,若需从这
人,若需从这 人进行问卷调查.设
人进行问卷调查.设 为选取的
为选取的 四所中学报名参加某高校今年自主招生的学生人数如下表所示:
四所中学报名参加某高校今年自主招生的学生人数如下表所示:



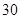



 名学生中随机抽取两名学生,求这两名学生自同一所中学的概率;
名学生中随机抽取两名学生,求这两名学生自同一所中学的概率; 两所中学的学生当中随机抽取两名学
两所中学的学生当中随机抽取两名学 表示抽得
表示抽得 表示抽到“好视力”学生的人数,求
表示抽到“好视力”学生的人数,求



 表示三位同学中取得参加数学竞赛复赛的资格的人数,求
表示三位同学中取得参加数学竞赛复赛的资格的人数,求 .
.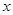 ,
, 的含量(单位:毫克)下表是乙厂的5件产品的测量数据:
的含量(单位:毫克)下表是乙厂的5件产品的测量数据: 且
且 为次品,从乙厂抽出的上述5件产品中,有放回的随机抽取1件产品,抽到次品则停止抽取,否则继续抽取,直到抽出次品为止,但抽取次数最多不超过3次,求抽取次数
为次品,从乙厂抽出的上述5件产品中,有放回的随机抽取1件产品,抽到次品则停止抽取,否则继续抽取,直到抽出次品为止,但抽取次数最多不超过3次,求抽取次数 的分布列及数学期望.
的分布列及数学期望.