题目内容
函数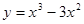 在
在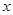 等于 处取得极小值.
等于 处取得极小值.
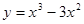 在
在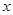 等于 处取得极小值.
等于 处取得极小值.2
试题分析:

 得
得 或
或 ,当
,当 时
时 ,当
,当 时
时 ,当
,当 时
时 ,所以
,所以 处取得极小值
处取得极小值点评:求函数极值点首先利用极值点处导数为零,求出所有导数为零的点,再判断这些点分成的区间内的单调性得到极大值点与极小值点

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
题目内容
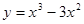 在
在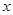 等于 处取得极小值.
等于 处取得极小值.
 得
得 或
或 ,当
,当 时
时 ,当
,当 时
时 ,当
,当 时
时 ,所以
,所以 处取得极小值
处取得极小值
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案