题目内容
(本小题满分16分)
设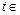 R,m,n都是不为1的正数,函数
R,m,n都是不为1的正数,函数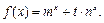
(1)若m,n满足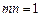 ,请判断函数
,请判断函数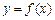 是否具有奇偶性. 如果具有,求出相
是否具有奇偶性. 如果具有,求出相
应的t的值;如果不具有,请说明理由;
(2)若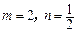 ,且
,且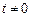 ,请判断函数
,请判断函数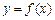 的图象是否具有对称性. 如果具
的图象是否具有对称性. 如果具
有,请求出对称轴方程或对称中心坐标;若不具有,请说明理由.
设
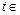 R,m,n都是不为1的正数,函数
R,m,n都是不为1的正数,函数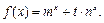
(1)若m,n满足
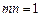 ,请判断函数
,请判断函数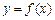 是否具有奇偶性. 如果具有,求出相
是否具有奇偶性. 如果具有,求出相应的t的值;如果不具有,请说明理由;
(2)若
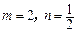 ,且
,且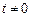 ,请判断函数
,请判断函数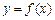 的图象是否具有对称性. 如果具
的图象是否具有对称性. 如果具有,请求出对称轴方程或对称中心坐标;若不具有,请说明理由.
(1) t =1
(2) 函数
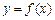 的图象是关于直线
的图象是关于直线 对称的轴对称图形
对称的轴对称图形(1)因为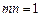 ,所以
,所以 ……………………2分
……………………2分
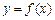 是偶函数
是偶函数 恒成立
恒成立 恒成立. ………4分
恒成立. ………4分
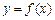 是奇函数
是奇函数 恒成立
恒成立 恒成立. ………6分
恒成立. ………6分
因为m,n都是不为1的正数,且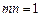 ,所以
,所以 ,
,
故当且仅当t =1时,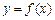 是偶函数;当且仅当
是偶函数;当且仅当 时,
时,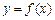 是奇函数.
是奇函数.
………………………8分
(2)当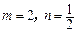 时,
时, .
.
如果 ,那么
,那么 ,
,
于是有 ,
,
所以函数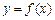 的图象是关于点
的图象是关于点 对称的中心对称图形. …………12分
对称的中心对称图形. …………12分
如果 ,那么
,那么 ,
,
于是有 ,
,
所以函数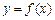 的图象是关于直线
的图象是关于直线 对称的轴对称图形. ……………16分
对称的轴对称图形. ……………16分
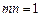 ,所以
,所以 ……………………2分
……………………2分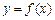 是偶函数
是偶函数 恒成立
恒成立 恒成立. ………4分
恒成立. ………4分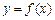 是奇函数
是奇函数 恒成立
恒成立 恒成立. ………6分
恒成立. ………6分因为m,n都是不为1的正数,且
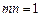 ,所以
,所以 ,
,故当且仅当t =1时,
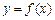 是偶函数;当且仅当
是偶函数;当且仅当 时,
时,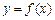 是奇函数.
是奇函数.………………………8分
(2)当
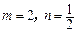 时,
时, .
.如果
 ,那么
,那么 ,
,于是有
 ,
,所以函数
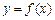 的图象是关于点
的图象是关于点 对称的中心对称图形. …………12分
对称的中心对称图形. …………12分如果
 ,那么
,那么 ,
,于是有
 ,
,所以函数
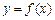 的图象是关于直线
的图象是关于直线 对称的轴对称图形. ……………16分
对称的轴对称图形. ……………16分
练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
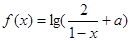 是奇函数,则使
是奇函数,则使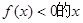 的取值范围是
的取值范围是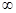 ,0)
,0)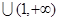
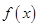 是奇函数,当
是奇函数,当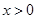 时,
时,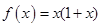 ;当
;当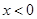 时,
时,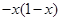
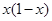

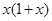
 是R上的奇函数,且当
是R上的奇函数,且当 时,
时, ,
, 等于 ( )
等于 ( )


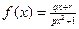 有最大值
有最大值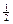 , 且
, 且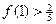 , 其中实数
, 其中实数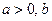 是正整数.
是正整数.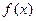 的解析式;
的解析式;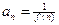 , 证明
, 证明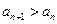 (
(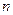 是正整数).
是正整数). 是奇函数,当
是奇函数,当 时
时 ,当
,当 时
时



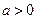 ,且
,且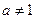 ,
,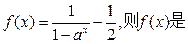
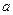 有关
有关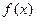 既是奇函数,又是周期为3的周期函数,当
既是奇函数,又是周期为3的周期函数,当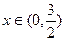 时,
时,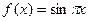 ,
,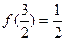 ,则函数
,则函数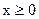 时,
时,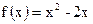 , 则
, 则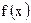 在
在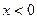 时的解析式是 _______________
时的解析式是 _______________