Question

已知函数f(x)=

lnx

x

，
（1）求函数f（x）的单调区间；
（2）设a＞0，求函数f（x）在[2a，4a]上的最小值．

Answer 1

（1）定义域为（0，+∞），f′(x)=

1-lnx

x2

，令f′(x)=

1-lnx

x2

=0，则x=e，
当x变化时，f′（x），f（x）的变化情况如下表：



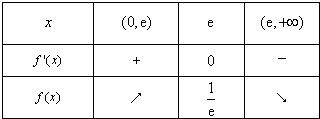
∴f（x）的单调增区间为（0，e）；单调减区间为（e，+∞）．
（2）由（1）知f（x）在（0，e）上单调递增，在（e，+∞）上单调递减，所以，
当4a≤e时，即0＜a≤

e

4

时，f（x）在[2a，4a]上单调递增，
∴f（x）_min=f（2a）=

ln(2a)

2a

；
当2a≥e时，即a≥

e

2

f（x）在[2a，4a]上单调递减，∴f（x）_min=f（4a）=

ln(4a)

4a

当2a＜e＜4a时，即

e

4

＜a＜

e

2

时，f（x）在[2a，e]上单调递增，f（x）在[e，4a]上单调递减，
∴f（x）_min=min{f（2a），f（4a）}．下面比较f（2a），f（4a）的大小，
∵f(2a)-f(4a)=

lna

4a

，
∴若

e

4

＜a≤1，则f（a）-f（2a）≤0，此时f(x)min=f(2a)=

ln2a

2a

；
若1＜a＜

e

2

，则f（a）-f（2a）＞0，此时f(x)min=f(4a)=

ln4a

4a

；
综上得：当0＜a≤1时，f(x)min=f(2a)=

ln2a

2a

；
当a＞1时，f(x)min=f(4a)=

ln4a

4a

．