题目内容
设函数

 .
.
(1)当 时,解关于
时,解关于 的不等式
的不等式 ;
;
(2)如果 ,
, ,求
,求 的取值范围.
的取值范围.
(1) ;(2)
;(2)
【解析】
试题分析:(1)理解绝对值的几何意义, 表示的是数轴的上点
表示的是数轴的上点 到原点的距离;(2)对
到原点的距离;(2)对 分类讨论,分
分类讨论,分 三部分进行讨论;(3)掌握一般不等式的解法:
三部分进行讨论;(3)掌握一般不等式的解法: ,
, .(4)对于恒成立的问题,常用到以下两个结论:(1)
.(4)对于恒成立的问题,常用到以下两个结论:(1) ,(2)
,(2) .
.
试题解析:解:(1)当 时,原不等式可变为
时,原不等式可变为 ,
,
可得其解集为 4分
4分
(2)因 对任意
对任意 都成立.
都成立.
∴ 对任何
对任何 都成立.
都成立.
∵ 解集为
解集为 .∴
.∴ 8分
8分
考点:(1)含绝对值不等式的解法;(2)恒成立的问题.

练习册系列答案
相关题目

 (a>0,b>0)的左、右焦点,过F1的直线
(a>0,b>0)的左、右焦点,过F1的直线 与
与 的左、右两支分别交于A,B两点.若 | AB | : | BF2 | : | AF2 |=3:4 : 5,则双曲线的离心率为( )
的左、右两支分别交于A,B两点.若 | AB | : | BF2 | : | AF2 |=3:4 : 5,则双曲线的离心率为( ) B.
B. C.2 D.
C.2 D.

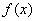 是定义在
是定义在 上的非负可导函数,且满足
上的非负可导函数,且满足 ,对任意正数
,对任意正数 ,若
,若 ,则必有( )
,则必有( ) B.
B.
 D.
D.

 在
在 处取得极值
处取得极值 ,其中
,其中 为常数.
为常数. ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围. ,
, ,则
,则 ( )
( ) |0<
|0< } B.{
} B.{