Question

在极坐标系中，由极点向直线l引垂线，垂足为点A(4，

π

4

)，则直线l的极坐标方程为

 

．

Answer 1

分析：此题可直接在极坐标系中求出直线l的极坐标方程．设直线l上任一点的极坐标为（ρ，θ），再结合直角三角形的边角关系即可求得ρ与θ的关系式即为所求直线l的极坐标方程．

解答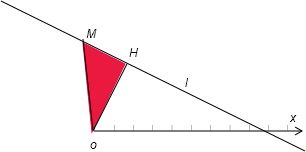：解：如图，
极点O向直线l作垂线，垂足是H，
设直线l上任一点的极坐标为（ρ，θ），
在直角三角形OHM中，∠HOM=ρ-

π

4

，
OH=OMcos∠HOM，
∴ρcos(θ-

π

4

)=4
故答案为：ρcos（θ-

π

4

）=4．

点评：本题考查简单曲线的极坐标方程，能在极坐标系中用极坐标刻画点的位置，体会在极坐标系和平面直角坐标系中刻画点的位置的区别，能进行极坐标和直角坐标的互化．