题目内容
(理)已知数列{log3(an+1)}(n∈N*)为等差数列,且a1=2,a2=8,则
(
+
+
+…+
)等于( )
| lim |
| x→∞ |
| 1 |
| a2-a1 |
| 1 |
| a3-a2 |
| 1 |
| a4-a3 |
| 1 |
| an+1-an |
分析:由题意,可先由数列{log3(an+1)}(n∈N*)为等差数列,且a1=2,a2=8得出数列{log2(an-1)}的首项为1,公差为1,由此解出log3(an-1)=1+(n-1)×1=n,从而求出an=-1+2n,再研究an+1-an=2n+1-1-2n+1=2n即可得出
(
+
+…+
)=
(
+
+…+
),结合等比数列的求和公式计算出所求的极限即可
| lim |
| n→∞ |
| 1 |
| a2-a1 |
| 1 |
| a3-a2 |
| 1 |
| an+1-an |
| lim |
| n→∞ |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
解答:解:数列{log3(an+1)}(n∈N*)为等差数列,且a1=2,a2=8
数列的公差为log39-log33=1,
故log3(an+1)=1+(n-1)×1=n,即an+1=2n,an=-1+2n,
∴an+1-an=2n+1-1-2n+1=2n
∴
(
+
+…+
)=
(
+
+…+
)=
(
)=
(1-
)=1
故答案为1
数列的公差为log39-log33=1,
故log3(an+1)=1+(n-1)×1=n,即an+1=2n,an=-1+2n,
∴an+1-an=2n+1-1-2n+1=2n
∴
| lim |
| n→∞ |
| 1 |
| a2-a1 |
| 1 |
| a3-a2 |
| 1 |
| an+1-an |
| lim |
| n→∞ |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
| lim |
| n→∞ |
| ||||
1-
|
| lim |
| n→∞ |
| 1 |
| 2n |
故答案为1
点评:本题考查数列与极限的综合,考查了等差数列的性质,通项公式,对数的运算,等比数列的求和等,涉及到的知识点多,综合性强,解题的关键是由题设条件求出an=-1+2n,难度较高.

练习册系列答案
相关题目
 等于
等于


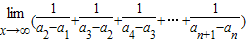 等于( )
等于( )

