题目内容

在平面直角坐标系xOy中，点P（x，y）是椭圆 $数学公式$ 上的一个动点，求S=x+y的最大值．

解：因椭圆 $\text{[math]}$ 的参数方程为 $\text{[math]}$ （?为参数）
故可设动点P的坐标为 $\text{[math]}$ ，其中0≤?＜2π．
因此 $\text{[math]}$
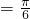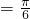所以，当 $\text{[math]}$ 时，S取最大值2．
分析：先根据椭圆的标准方程进行三角代换表示椭圆上任意一点，然后利用三角函数的辅助角公式进行化简，即可求出所求．
点评：本题主要考查了椭圆的简单性质及参数方程的问题．考查了学生综合分析问题和解决问题的能力．

练习册系列答案

名师点津系列答案

零失误分层训练系列答案

黄冈密卷系列答案

自主创新课时作业系列答案

世纪金榜金榜小博士系列答案

培优竞赛超级课堂系列答案

黄冈小状元达标卷系列答案

黄冈冠军课课练系列答案

高效精练系列答案

练与测联动课堂系列答案

相关题目

在平面直角坐标系xOy中，点P到点F（3，0）的距离的4倍与它到直线x=2的距离的3倍之和记为d，当P点运动时，d恒等于点P的横坐标与18之和
（Ⅰ）求点P的轨迹C；
（Ⅱ）设过点F的直线I与轨迹C相交于M，N两点，求线段MN长度的最大值．

在平面直角坐标系xOy中，点P（

，cos²θ）在角α的终边上，点Q（sin²θ，-1）在角β的终边上，且

．
（1）求cos2θ；
（2）求sin（α+β）的值．

在平面直角坐标系xOy中，点P的直角坐标为(1，-

)、若以原点O为极点，x轴正半轴为极轴建立极坐标系，则点P的极坐标可以是（　　）

（2011•太原模拟）在平面直角坐标系xOy中，点P（x，y）是椭圆

+y²=1上的一个动点，则S=x+y的最大值为

在平面直角坐标系xOy中，点_P到定点F（-1，0）的距离的两倍和它到定直线x=-4的距离相等．
（Ⅰ）求点P的轨迹C的方程，并说明轨迹C是什么图形；
（Ⅱ）已知点Q（l，1），直线l：y=x+m（m∈R）和轨迹C相交于A、B两点，是否存在实数m，使△ABQ的面积S最大？若存在，求出m的值；若不存在，说明理由．