题目内容
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分8分,第3小题满分6分.
已知负数![]() 和正数
和正数![]() ,且对任意的正整数n,当
,且对任意的正整数n,当![]() ≥0时, 有[
≥0时, 有[![]() ,
, ![]() ]=
]=
[![]() ,
, ![]() ];当
];当![]() <0时, 有[
<0时, 有[![]() ,
, ![]() ]= [
]= [![]() ,
, ![]() ].
].
(1)求证数列{![]() }是等比数列;
}是等比数列;
(2)若![]() ,求证
,求证![]()
![]() ;
;
(3)是否存在![]() ,使得数列
,使得数列![]() 为常数数列?请说明理由.
为常数数列?请说明理由.
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分8分,第3小题满分6分.
(1)当≥0时,bn+1-an+1= -an= ;
当<0, bn+1-an+1 = bn- = .
所以,总有bn+1-an+1 = (bn-an),
又![]() ,可得
,可得![]() ,
,
所以数列{bn-an}是等比数列. ………………4分
(2)①由![]() ,可得
,可得![]() ,故有
,故有![]() ,
,
∴![]() ,
,![]() ,从而
,从而![]() ,
,
故当n=1时,![]() 成立. ………………6分
成立. ………………6分
②假设当![]() 时,
时,![]() 成立,即
成立,即![]() ,
,
由![]() ,可得
,可得![]() ,
,
![]() , 故有
, 故有![]() ,
,
∴![]() , ………………9分
, ………………9分
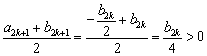 ,故有
,故有![]()
∴![]() ,
, ![]() ,故
,故![]()
∴当![]() 时,
时,![]() 成立.
成立.
综合①②可得对一切正整数n,都有![]() . ………………12分
. ………………12分
(3)假设存在![]() ,使得数列
,使得数列![]() 为常数数列,
为常数数列,
由(1)可得bn-an=![]() ()n-1,又
()n-1,又![]() ,
,
故bn=![]() ()n-1, ………………14分
()n-1, ………………14分
由![]() 恒成立,可知≥0,即
恒成立,可知≥0,即![]() ()n ≥0恒成立,
()n ≥0恒成立,
即2n≤![]() 对任意的正整数n恒成立, ………………16分
对任意的正整数n恒成立, ………………16分
又![]() 是正数,故n≤
是正数,故n≤![]() 对任意的正整数n恒成立,
对任意的正整数n恒成立,
因为![]() 是常数,故n≤
是常数,故n≤![]() 不可能对任意正整数n恒成立.
不可能对任意正整数n恒成立.
故不存在![]() ,使得数列
,使得数列![]() 为常数数列. ………………18分
为常数数列. ………………18分

 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且 .设
.设 .
. ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集; 且法向量为
且法向量为 的直线
的直线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若 恒成立,求实数
恒成立,求实数 的最大值;
的最大值; 、
、 和
和 的值. 当
的值. 当 对称,且在
对称,且在 处
处 中,
中,
 项和
项和 ;
; 项和为
项和为 ,若
,若 对任意
对任意 恒成立,求
恒成立,求 的最小值.
的最小值. 是定义域为R的奇函数.
是定义域为R的奇函数. 时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集; 恒成立的
恒成立的 的取值范围;
的取值范围; 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且 .设
.设 .
. ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集; 且法向量为
且法向量为 的直线
的直线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若 恒成立,求实数
恒成立,求实数 的最大值;
的最大值; 、
、 和
和 的值. 当
的值. 当 对称,且在
对称,且在 处
处