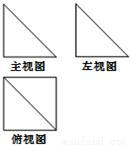
题目内容
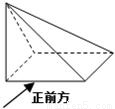
已知底面为正方形的四棱锥P-ABCD中,PA⊥面ABCD,PA=AB=AD=2,则点C到平面PBD的距离为( )A.
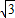
B.
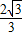
C.

D.1
【答案】分析:建立空间直角坐标系,求出平面PBD的法向量,再求出平面的斜线PC所在的向量 ,然后求出
,然后求出 在法向量上的射影即可得到点到平面的距离.
在法向量上的射影即可得到点到平面的距离.
解答: 解:建立如图所示的直角坐标系,
解:建立如图所示的直角坐标系,
则A(0,0,0)、D(0,2,0)、P(0,0,2).
在Rt△BAD中,AD=2,BD=2 ,
,
∴AB=2.∴B(2,0,0)、C(2,2,0),
所以 =(2,0,-2),
=(2,0,-2), =(0,2,-2),
=(0,2,-2),
设平面PBD的法向量为 =(x,y,z),
=(x,y,z),
则 =0,
=0, =0,即
=0,即 ,
,
∴x=y=z,故可取为 =(1,1,1).
=(1,1,1).
∵ =(2,2,-2),
=(2,2,-2),
∴C到面PBD的距离为d=| |=
|= .
.
故选B.
点评:解决此类问题的关键是熟悉几何体的结构特征,以便建立空间直角坐标系利用向量的基本运算解决线面共线、空间角与空间距离等问题.
 ,然后求出
,然后求出 在法向量上的射影即可得到点到平面的距离.
在法向量上的射影即可得到点到平面的距离.解答:
 解:建立如图所示的直角坐标系,
解:建立如图所示的直角坐标系,则A(0,0,0)、D(0,2,0)、P(0,0,2).
在Rt△BAD中,AD=2,BD=2
 ,
,∴AB=2.∴B(2,0,0)、C(2,2,0),
所以
 =(2,0,-2),
=(2,0,-2), =(0,2,-2),
=(0,2,-2),设平面PBD的法向量为
 =(x,y,z),
=(x,y,z),则
 =0,
=0, =0,即
=0,即 ,
,∴x=y=z,故可取为
 =(1,1,1).
=(1,1,1).∵
 =(2,2,-2),
=(2,2,-2),∴C到面PBD的距离为d=|
 |=
|= .
.故选B.
点评:解决此类问题的关键是熟悉几何体的结构特征,以便建立空间直角坐标系利用向量的基本运算解决线面共线、空间角与空间距离等问题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
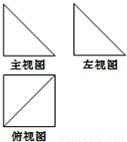
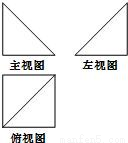
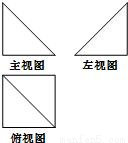
 15、如图,已知底面为正方形的四棱锥,其一条侧棱垂直于底面,那么该四棱锥的三视图是下列各图中的( )
15、如图,已知底面为正方形的四棱锥,其一条侧棱垂直于底面,那么该四棱锥的三视图是下列各图中的( )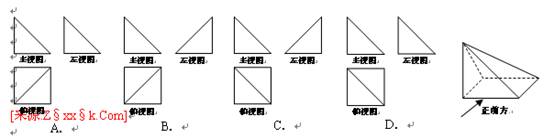 [来源:Z§xx§k.Com]
[来源:Z§xx§k.Com]