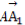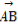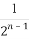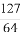题目内容
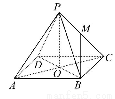
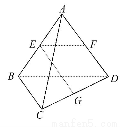
如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E,F,G分别是AB,AD,CD的中点,计算:
(1)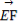 ·
·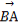 .
.
(2)EG的长.
(3)异面直线EG与AC所成角的大小.
(1) 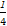 (2)
(2)  (3) 45°
(3) 45°
【解析】设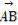 =a,
=a,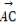 =b,
=b,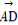 =c,
=c,
则|a|=|b|=|c|=1,
<a,b>=<b,c>=<c,a>=60°,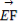 =
=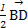 =
=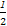 c-
c-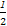 a,
a,
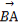 =-a,
=-a,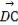 =b-c.
=b-c.
(1)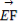 ·
·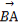 =(
=(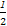 c-
c-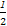 a)·(-a)
a)·(-a)
=-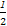 a·c+
a·c+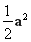 =-
=-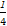 +
+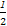 =
=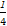 .
.
(2)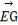 =
=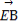 +
+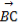 +
+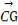
=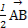 +(
+(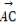 -
-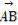 )+
)+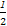 (
(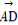 -
-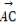 )
)
=-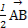 +
+ +
+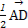 =-
=-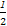 a+
a+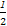 b+
b+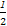 c
c
∴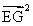 =
=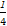 (-a+b+c)2
(-a+b+c)2
=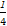 (
(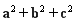 -2a·b-2a·c+2b·c)=
-2a·b-2a·c+2b·c)=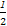 ,
,
∴|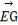 |=
|= ,即EG的长为
,即EG的长为 .
.
(3)由(2)知,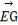 ·
·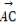 =(-
=(-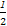 a+
a+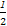 b+
b+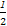 c)·b
c)·b
=-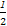 a·b+
a·b+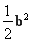 +
+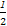 c·b=
c·b=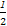 ,
,
∴cos<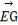 ,
,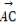 >=
>=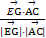 =
=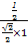 =
= .
.
故异面直线EG与AC所成的角为45°.
【方法技巧】用向量法解题的常见类型及常用方法
1.常见类型
利用向量可解决空间中的平行、垂直、长度、夹角等问题.
2.常用的解题方法
(1)基向量法
先选择一组基向量,把其他向量都用基向量表示,然后根据向量的运算解题.
(2)坐标法
根据条件建立适当的空间直角坐标系,并求出相关点的坐标,根据向量的坐标运算解题即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目