题目内容
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的最小正周期为π,当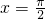 时,f(x)取得最小值-2.
时,f(x)取得最小值-2.
(Ⅰ)求f(x)的解析式;
(Ⅱ)在△ABC中,若f(A)=-1,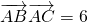 ,求边BC的最小值..
,求边BC的最小值..
解:(Ⅰ)依题意得,A=2,函数f(x)的周期为π,∵ω>0,∴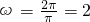 .(3分)
.(3分)
又 ,∴
,∴ ,∵0<φ<π,∴
,∵0<φ<π,∴ ,(5分)
,(5分)
∴ .(6分)
.(6分)
(Ⅱ)∵ ,0<2A<2π,∴
,0<2A<2π,∴ ,或
,或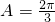 .(8分)
.(8分)
又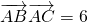 ,即
,即 ,∴
,∴ ,|AB|•|AC|=12.(9分)
,|AB|•|AC|=12.(9分)
∵|BC|2=|AB|2+|AC|2-2|AB|•|AC|cosA=|AB|2+|AC|2-|AB|•|AC|≥|AB|•|AC|=12,
∴BC的最小值为 .(12分)
.(12分)
分析:(Ⅰ)根据函数的最值求出A=2,根据函数f(x)的周期求出ω,再由当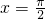 时,f(x)取得最小值-2,求出φ,从而
时,f(x)取得最小值-2,求出φ,从而
得到f(x)的解析式.
(Ⅱ) f(A)=-1 求得A,再由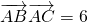 ,进一步确定A的值,利用余弦定理求出边BC的最小值.
,进一步确定A的值,利用余弦定理求出边BC的最小值.
点评:本题考查三角函数的周期性及其求法,两个向量的数量积的定义,三角函数的最值、余弦定理的应用,求出函数的解析式
是解题的突破口.
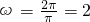 .(3分)
.(3分)又
 ,∴
,∴ ,∵0<φ<π,∴
,∵0<φ<π,∴ ,(5分)
,(5分)∴
 .(6分)
.(6分)(Ⅱ)∵
 ,0<2A<2π,∴
,0<2A<2π,∴ ,或
,或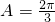 .(8分)
.(8分)又
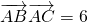 ,即
,即 ,∴
,∴ ,|AB|•|AC|=12.(9分)
,|AB|•|AC|=12.(9分)∵|BC|2=|AB|2+|AC|2-2|AB|•|AC|cosA=|AB|2+|AC|2-|AB|•|AC|≥|AB|•|AC|=12,
∴BC的最小值为
 .(12分)
.(12分)分析:(Ⅰ)根据函数的最值求出A=2,根据函数f(x)的周期求出ω,再由当
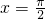 时,f(x)取得最小值-2,求出φ,从而
时,f(x)取得最小值-2,求出φ,从而得到f(x)的解析式.
(Ⅱ) f(A)=-1 求得A,再由
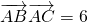 ,进一步确定A的值,利用余弦定理求出边BC的最小值.
,进一步确定A的值,利用余弦定理求出边BC的最小值.点评:本题考查三角函数的周期性及其求法,两个向量的数量积的定义,三角函数的最值、余弦定理的应用,求出函数的解析式
是解题的突破口.

练习册系列答案
相关题目