题目内容
已知命题p：关于x的方程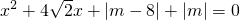
有实根；命题q：函数
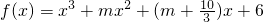在R上有极值；若命题“p且q”为真，求实数m的取值范围．
解：关于x的方程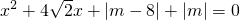有实根∴△=32-4（|m-8|+|m|）≥0∴|m-8|+|m|≤8
又∵|m-8|+|m|≥|m-8-m|=8
故p为真时：0≤m≤8
当命题q为真时：
（8分）∴m2-3m-10＞0
故m＞5或m＜-2
当命题p且q为真：m∈（5，8]
分析：由已知命题“p且q”为真 则p，q均为真命题． 分别求出p，q为真命题时，m的取值范围，两部分取公共部分即可．
点评：本题考查复合命题真假性的条件．一般转化为简单命题的真假去解决，考查转化、逻辑思维、计算的能力．
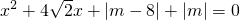有实根∴△=32-4（|m-8|+|m|）≥0∴|m-8|+|m|≤8又∵|m-8|+|m|≥|m-8-m|=8
故p为真时：0≤m≤8
当命题q为真时：
（8分）∴m2-3m-10＞0故m＞5或m＜-2
当命题p且q为真：m∈（5，8]
分析：由已知命题“p且q”为真 则p，q均为真命题． 分别求出p，q为真命题时，m的取值范围，两部分取公共部分即可．
点评：本题考查复合命题真假性的条件．一般转化为简单命题的真假去解决，考查转化、逻辑思维、计算的能力．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
已知命题p：“关于x的方程x2-ax+a=0无实根”和命题q：“函数f（x）=x2-ax+a在区间[-1，+∞）上单调．如果命题p∨q是假命题，那么，实数a的取值范围是（ ）
| A、（0，4） | B、（-∞，2]∪（0，4） | C、（-2，0]∪[4，+∞） | D、[-2，0）∪（4，+∞） |