题目内容
已知全集U=R,A={x|-
x2+x+1＞0},B={x|3x2-4x+1＞0},求
(A∩B).
解：A={x|-
x2+x+1＞0}={x|3x2-4x-4＜0}={x|-
＜x＜2};
B={x|3x2-4x+1＞0}={x|x＜
或x＞1}.
如下图.
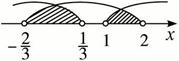
得A∩B={x|-
＜x＜
或1＜x＜2}.
所以
(A∩B)={x|x≤-
或
≤x≤1或x≥2}.
练习册系列答案
相关题目
x2+x+1＞0},B={x|3x2-4x+1＞0},求(A∩B).
},那么A∩B=____________,A∩B∩(
P)=___________. 
∈Z},B={x|x2-17x+16＞0},则A∩
B=_________.
，则C=( )
B.
C.
D.
B=
则
为
（
）
B、
C、
D、
A)∩(
B).