题目内容
已知奇函数f（x）在区间[0，+∞）上单调递减，则满足f（2x-1）+f（x+3）＜0的x的取值范围是________．
（-
）
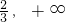分析：由奇函数对称区间上的单调性相同可知，f（x）在区间（-∞，0）上单调递减，即f（x）在（-∞，+∞）上单调递减，结合奇函数的定义可知f（2x-1）＜f（-x-3），从而可求
解答：∵奇函数f（x）在区间[0，+∞）上单调递减，
则f（x）在区间（-∞，0）上单调递减，即f（x）在（-∞，+∞）上单调递减
∵f（2x-1）+f（x+3）＜0
∴f（2x-1）＜-f（x+3）=f（-x-3）
∴2x-1＞-x-3
解可得，x
故答案为：（-）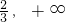
点评：本题考查了函数的奇偶性，函数的单调性，奇函数对称区间上单调性性质的应用，将已知不等式转化为f（2x-1）＜f（-x-3）是解答本题的关键
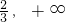）分析：由奇函数对称区间上的单调性相同可知，f（x）在区间（-∞，0）上单调递减，即f（x）在（-∞，+∞）上单调递减，结合奇函数的定义可知f（2x-1）＜f（-x-3），从而可求
解答：∵奇函数f（x）在区间[0，+∞）上单调递减，
则f（x）在区间（-∞，0）上单调递减，即f（x）在（-∞，+∞）上单调递减
∵f（2x-1）+f（x+3）＜0
∴f（2x-1）＜-f（x+3）=f（-x-3）
∴2x-1＞-x-3
解可得，x
故答案为：（-
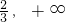）点评：本题考查了函数的奇偶性，函数的单调性，奇函数对称区间上单调性性质的应用，将已知不等式转化为f（2x-1）＜f（-x-3）是解答本题的关键
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
已知奇函数f（x）在x≥0时的图象是如图所示的抛物线的一部分，已知奇函数f（x）在[-1，0]上单调递减，又α，β为锐角三角形的两内角，则有（ ）
| A、f（sinα-sinβ）≥f（cosα-cosβ） | B、f（sinα-cosβ）＞f（cosα-sinβ） | C、f（sinα-cosβ）≥f（cosα-sinβ） | D、f（sinα-cosβ）＜f（cosα-sinβ） |