题目内容
若曲线y=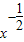 在点(a,
在点(a,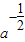 )处的切线与两个坐标围成的三角形的面积为18,则a=( )
)处的切线与两个坐标围成的三角形的面积为18,则a=( )A.64
B.32
C.16
D.8
【答案】分析:欲求参数a值,必须求出在点(a,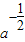 )处的切线方程,只须求出其斜率的值即可,故先利用导数求出在x=a处的导函数值,再结合导数的几何意义即可求出切线的斜率得到切线的方程,最后求出与坐标轴的交点坐标结合三角形的面积公式.从而问题解决.
)处的切线方程,只须求出其斜率的值即可,故先利用导数求出在x=a处的导函数值,再结合导数的几何意义即可求出切线的斜率得到切线的方程,最后求出与坐标轴的交点坐标结合三角形的面积公式.从而问题解决.
解答:解:y′=-
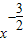 ,∴k=-
,∴k=-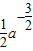 ,
,
切线方程是y-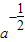 =-
=-
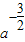 (x-a),
(x-a),
令x=0,y=
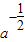 ,令y=0,x=3a,
,令y=0,x=3a,
∴三角形的面积是s= •3a•
•3a•
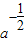 =18,
=18,
解得a=64.
故选A.
点评:本试题主要考查求导法则、导数的几何意义、切线的求法和三角形的面积公式,考查考生的计算能力.
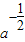 )处的切线方程,只须求出其斜率的值即可,故先利用导数求出在x=a处的导函数值,再结合导数的几何意义即可求出切线的斜率得到切线的方程,最后求出与坐标轴的交点坐标结合三角形的面积公式.从而问题解决.
)处的切线方程,只须求出其斜率的值即可,故先利用导数求出在x=a处的导函数值,再结合导数的几何意义即可求出切线的斜率得到切线的方程,最后求出与坐标轴的交点坐标结合三角形的面积公式.从而问题解决.解答:解:y′=-

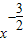 ,∴k=-
,∴k=-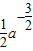 ,
,切线方程是y-
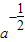 =-
=-
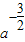 (x-a),
(x-a),令x=0,y=

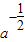 ,令y=0,x=3a,
,令y=0,x=3a,∴三角形的面积是s=
 •3a•
•3a•
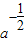 =18,
=18,解得a=64.
故选A.
点评:本试题主要考查求导法则、导数的几何意义、切线的求法和三角形的面积公式,考查考生的计算能力.

练习册系列答案
相关题目
 在点(a,
在点(a, )处的切线与两个坐标围成的三角形的面积为18,则a=( )
)处的切线与两个坐标围成的三角形的面积为18,则a=( ) 在点(a,
在点(a, )处的切线与两个坐标围成的三角形的面积为18,则a=( )
)处的切线与两个坐标围成的三角形的面积为18,则a=( ) 在点(a,
在点(a, )处的切线与两个坐标围成的三角形的面积为18,则a=( )
)处的切线与两个坐标围成的三角形的面积为18,则a=( ) 在点(a,
在点(a, )处的切线与两个坐标围成的三角形的面积为18,则a=( )
)处的切线与两个坐标围成的三角形的面积为18,则a=( ) 在点(a,
在点(a, )处的切线与两个坐标围成的三角形的面积为18,则a=( )
)处的切线与两个坐标围成的三角形的面积为18,则a=( )