题目内容
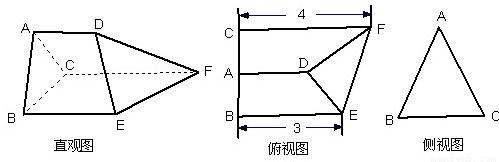
如图是某三棱柱被削去一个底面后的直观图与侧视图、俯视图.已知CF=2AD,侧视图是边长为2的等边三角形;俯视图是直角梯形,有关数据如图所示.(Ⅰ)求该几何体的体积;
(Ⅱ)求二面角B-DE-F的余弦值.

【答案】分析:(Ⅰ)取CF中点P,过P作PQ∥CB交BE于Q,连接PD,QD,该几何体的体积V=V三棱柱PDQ-ABC+VD-EFPQ然后求解即可.
(Ⅱ)取BC中点O,EF中点R,连接OA,OR,以O为原点,OB,OR,OA所在直线分别为x,y,z轴.建立空间直角坐标系,求平面ABED的法向量 ,平面DEF的法向量为
,平面DEF的法向量为 ,利用
,利用 求二面角B-DE-F的余弦值.
求二面角B-DE-F的余弦值.
解答:解:(Ⅰ)取CF中点P,过P作PQ∥CB交BE于Q,
连接PD,QD,AD∥CP,且AD=CP.四边形ACPD为平行四边形,
∴AC∥PD,∴平面PDQ∥面ABC.
∴ ;(5分)
;(5分)
(Ⅱ)取BC中点O,EF中点R,连接OA,OR.
则OA⊥BC,∴OA⊥平面BCFE,OA⊥OR.
又∵OR⊥BC,以O为原点,OB,OR,OA所在直线分别为x,y,z轴,
建立空间直角坐标系,则B(1,0,0),D(0,2, ),E(1,3,0),F(-1,4,0)
),E(1,3,0),F(-1,4,0)
设平面DEF的法向量为
∵ ∵
∵
∴
令
设平面ABED的法向量
∵
 ,∴
,∴
令
∴ ∴
∴ =
= ,
,
显然二面角B-DE-F的平面角为钝角,
所以二面角B-DE-F的余弦值为 .(12分)
.(12分)
点评:本题考查三视图求体积,求几何体的二面角,考查学生空间想象能力,逻辑思维能力,是中档题.
(Ⅱ)取BC中点O,EF中点R,连接OA,OR,以O为原点,OB,OR,OA所在直线分别为x,y,z轴.建立空间直角坐标系,求平面ABED的法向量
 ,平面DEF的法向量为
,平面DEF的法向量为 ,利用
,利用 求二面角B-DE-F的余弦值.
求二面角B-DE-F的余弦值.解答:解:(Ⅰ)取CF中点P,过P作PQ∥CB交BE于Q,
连接PD,QD,AD∥CP,且AD=CP.四边形ACPD为平行四边形,
∴AC∥PD,∴平面PDQ∥面ABC.
∴
 ;(5分)
;(5分)(Ⅱ)取BC中点O,EF中点R,连接OA,OR.
则OA⊥BC,∴OA⊥平面BCFE,OA⊥OR.
又∵OR⊥BC,以O为原点,OB,OR,OA所在直线分别为x,y,z轴,
建立空间直角坐标系,则B(1,0,0),D(0,2,
 ),E(1,3,0),F(-1,4,0)
),E(1,3,0),F(-1,4,0)设平面DEF的法向量为

∵
 ∵
∵
∴

令

设平面ABED的法向量

∵

 ,∴
,∴
令

∴
 ∴
∴ =
= ,
,显然二面角B-DE-F的平面角为钝角,
所以二面角B-DE-F的余弦值为
 .(12分)
.(12分)点评:本题考查三视图求体积,求几何体的二面角,考查学生空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
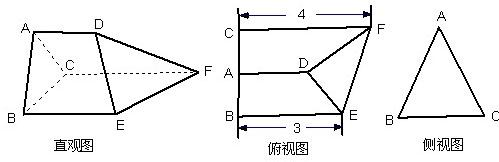
如图是某三棱柱被削去一个底面后的直观图与侧视图、俯视图.已知CF=2AD,侧视图是边长为2的等边三角形;俯视图是直角梯形,有关数据如图所示.
(Ⅰ)求该几何体的体积;
(Ⅱ)求二面角B-DE-F的余弦值.
(Ⅰ)求该几何体的体积;
(Ⅱ)求二面角B-DE-F的余弦值.

如图是某三棱柱被削去一个底面后的直观图与侧视图、俯视图.已知CF=2AD,侧视图是边长为2的等边三角形;俯视图是直角梯形,有关数据如图所示.
(Ⅰ)求该几何体的体积;
(Ⅱ)求二面角B-DE-F的余弦值.

(Ⅰ)求该几何体的体积;
(Ⅱ)求二面角B-DE-F的余弦值.