题目内容
设函数
，其中
，则导数f′（1）的取值范围是 ________
[
，2]
分析：先对函数进行求导，然后将x=1代入，再由两角和与差的公式进行化简，根据θ的范围和正弦函数的性质可求得最后答案．
解答：∵，
∴f'（x）=sinθx2+
cosθx
∴f′（1）=sinθ+cosθ=2sin（θ+
）
∵，∴θ+∈[，
]
∴sin（θ+）∈[
]
∴f′（1）∈[，2]
故答案为：[，2]．
点评：本题主要考查函数的求导运算和两角和与差的正弦公式的应用．考查基础知识的简单综合．高考对三角函数的考查以基础题为主，平时要注意基础知识的积累和基础题的练习．
，2]分析：先对函数
进行求导，然后将x=1代入，再由两角和与差的公式进行化简，根据θ的范围和正弦函数的性质可求得最后答案．解答：∵
，∴f'（x）=sinθx2+
cosθx∴f′（1）=sinθ+
cosθ=2sin（θ+）∵
，∴θ+∈[，]∴sin（θ+
）∈[]∴f′（1）∈[
，2]故答案为：[
，2]．点评：本题主要考查函数的求导运算和两角和与差的正弦公式的应用．考查基础知识的简单综合．高考对三角函数的考查以基础题为主，平时要注意基础知识的积累和基础题的练习．
练习册系列答案
相关题目
，其中
，则导数
的取值范围是
学科网
（B）. 
（C）
（D 
，其中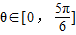
，则导数f'（-1）的取值范围（ ）
，其中
，则导数
的取值范围是（ ）
B．
C．
D．
，其中
，则导数
的取值范围是（ ）
B. 
C. 
D. 
，其中
，则导数
的取值范围是 
B. 
C.
D. 