题目内容

设0＜|a|≤2，函数f（x）=cos²x-|a|sinx-|b|的最大值为0，最小值为-4，且a与b的夹角为45°，求|a+b|.

解：f（x）=1-sin²x-|a|sinx-|b|

=-（sin²x+|a|sinx+）+1-|b|+=-（sinx+)²+1-|b|+)²,

∵0＜|a|²≤2，

∴当sinx=-时，f（x）取得最大值1-|b|+=0；

当sinx=1时，f（x）取得最小值-（|a|+|b|）=-4.

由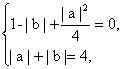

解得|a|=|b|=2.

所以|a+b|²=a²+2a·b+b²=8+4.

即|a+b|=2.

练习册系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

相关题目

已知函f（x）=ln x，g（x）=

ax²+bx（a≠0）．
（1）若a=-2时，函h（x）=f（x）-g（x），在其定义域是增函数，求b的取值范围；
（2）在（1）的结论下，设函数φ（x）=e^2x+be^x，x∈[0，ln2]，求函数φ（x）的最小值；
（3）当a=-2，b=4时，求证2x-f（x）≥g（x）-3．

x2-bx+c，x≤0

若f(-4)=f(0)，f(-2)=-2，则函数g（x）=f（x）-x的零点的个数为（　　）

已知函f（x）=e²+ax，g（x）=e^xlnx
（1）设曲线y=f（x）在x=1处得切线与直x+（e-1）y=1垂直，求a的值．
（2）若对任意实x≥0f（x）＞0恒成立，确定实数a的取值范围．
（3）a=1时，是否存x₀∈[1，e]，使曲线C：y=g（x）-f（x）在点x=x₀处得切线与y轴垂直？若存在求x₀的值，若不存在，请说明理由．

已知函f（x）=ln x，g（x）= $数学公式$ ax²+bx（a≠0）．
（1）若a=-2时，函h（x）=f（x）-g（x），在其定义域是增函数，求b的取值范围；
（2）在（1）的结论下，设函数φ（x）=e^2x+be^x，x∈[0，ln2]，求函数φ（x）的最小值；
（3）当a=-2，b=4时，求证2x-f（x）≥g（x）-3．

已知函f（x）=ln x，g（x）=

ax²+bx（a≠0）．
（1）若a=-2时，函h（x）=f（x）-g（x），在其定义域是增函数，求b的取值范围；
（2）在（1）的结论下，设函数φ（x）=e^2x+be^x，x∈[0，ln2]，求函数φ（x）的最小值；
（3）当a=-2，b=4时，求证2x-f（x）≥g（x）-3．