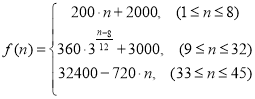题目内容
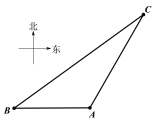
【题目】下图是一块平行四边形园地![]() ,经测量,
,经测量,![]()
![]() .拟过线段
.拟过线段![]() 上一点
上一点![]() 设计一条直路
设计一条直路![]() (点
(点![]() 在四边形
在四边形![]() 的边上,不计直路的宽度),将该园地分为面积之比为
的边上,不计直路的宽度),将该园地分为面积之比为![]() 的左,右两部分分别种植不同花卉.设
的左,右两部分分别种植不同花卉.设![]() (单位:m).
(单位:m).
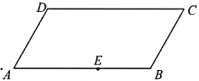
(1)当点![]() 与点
与点![]() 重合时,试确定点
重合时,试确定点![]() 的位置;
的位置;
(2)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)试确定点![]() 的位置,使直路
的位置,使直路![]() 的长度最短.
的长度最短.
【答案】(1)![]() 是
是![]() 的中点;(2)
的中点;(2)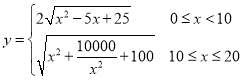 ;(3) 当
;(3) 当![]() ,
,![]() 时,
时,![]() 最短,其长度为
最短,其长度为![]() .
.
【解析】
(1)由![]() 可知
可知![]() ,从而证明
,从而证明![]() 是
是![]() 的中点.
的中点.
(2)求出平行四边形的面积为![]() ,进而可求
,进而可求![]() ,从而用
,从而用![]() 可将
可将![]() 表示出来,利用余弦定理即可得到
表示出来,利用余弦定理即可得到![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(3)当 ![]() ,由二次函数的性质可求最值;当
,由二次函数的性质可求最值;当![]() 时,由基本不等式可求最值.
时,由基本不等式可求最值.
解:(1)当点![]() 与点
与点![]() 重合时,由题设知,
重合时,由题设知,![]() .
.
于是![]() ,其中
,其中![]() 为平行四边形
为平行四边形![]() 边上的高.
边上的高.
得![]() ,即点
,即点![]() 是
是![]() 的中点.
的中点.
(2)因为点![]() 在线段
在线段![]() 上,所以
上,所以![]() .当
.当![]() 时,由(1)知
时,由(1)知
点![]() 在线段
在线段![]() 上.因为
上.因为![]()
所以![]() .
.
由![]() 得,
得,![]() .所以
.所以![]() 中,由余弦定理得
中,由余弦定理得
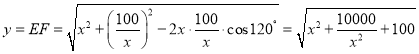 .
.
当![]() 时,点
时,点![]() 在线段
在线段![]() 上,由
上,由![]()
得![]() .当
.当![]() 时,
时,![]()
当![]() 时,
时,![]()
化简均为![]() .
.
综上,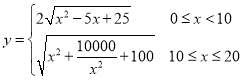 .
.
(3)当![]() 时,
时,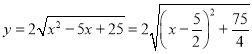 ,
,
于是当![]() 时,
时,![]() ,此时
,此时![]() .
.
当![]() 时,
时,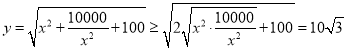
当且仅当![]() ,即
,即![]() 时,取等号
时,取等号
综上: 当![]() 距点
距点![]() ,
,![]() 距点
距点![]() 时,
时,![]() 最短,其长度为
最短,其长度为![]() .
.

练习册系列答案
相关题目