题目内容
函数f(x)=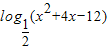 的值域 .
的值域 .
【答案】分析:利用复合函数的单调性求函数的值域.
解答:解:设t=g(x)=x2+4x-12,则由g(x)=x2+4x-12>0,得x>2或x<-6.
所以函数f(x)=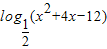 的值域为R.
的值域为R.
故答案为:R.
点评:本题主要考查对数函数的性质,比较基础.
解答:解:设t=g(x)=x2+4x-12,则由g(x)=x2+4x-12>0,得x>2或x<-6.
所以函数f(x)=
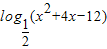 的值域为R.
的值域为R.故答案为:R.
点评:本题主要考查对数函数的性质,比较基础.

练习册系列答案
相关题目
命题p:?x∈(1,+∞),函数f(x)=|log2x|的值域为[0,+∞);命题q:?m≥0,使得y=sinmx的周期小于
,则( )
| π |
| 2 |
| A、p且q为假命题 |
| B、p或q为假命题 |
| C、非p为假命题 |
| D、非q为真命题 |