题目内容
已知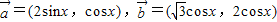 ,函数
,函数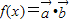
(1)求f(x)的最小正周期;
(2)当
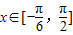 时,求f(x)的值域.
时,求f(x)的值域.
【答案】分析:(1)由向量数量积公式,并利用三角恒等变换化简得f(x)=2sin(2x+ )+1,由此可得f(x)的最小正周期;
)+1,由此可得f(x)的最小正周期;
(2)当 时,算出2x+
时,算出2x+ ∈
∈ .利用三角函数的图象与性质,即可算出f(x)的值域.
.利用三角函数的图象与性质,即可算出f(x)的值域.
解答:解:(1)∵ ,
,
∴函数 =2
=2 sinxcosx+2cos2x
sinxcosx+2cos2x
= sin2x+(1+cos2x)=2sin(2x+
sin2x+(1+cos2x)=2sin(2x+ )+1
)+1
∴f(x)的最小正周期T= =π;
=π;
(2)∵ 时,2x+
时,2x+ ∈
∈
∴当x= 或
或 时,函数有最小值0;当x=
时,函数有最小值0;当x= 时,函数有最大值为3
时,函数有最大值为3
当 时,f(x)的值域的值域为[0,3].
时,f(x)的值域的值域为[0,3].
点评:本题给出向量含有三函数的坐标,求函数的周期与值域.着重考查了向量的数量积、三角恒等变换公式和三角函数的图象与性质等知识,属于中档题.
 )+1,由此可得f(x)的最小正周期;
)+1,由此可得f(x)的最小正周期;(2)当
 时,算出2x+
时,算出2x+ ∈
∈ .利用三角函数的图象与性质,即可算出f(x)的值域.
.利用三角函数的图象与性质,即可算出f(x)的值域.解答:解:(1)∵
 ,
,∴函数
 =2
=2 sinxcosx+2cos2x
sinxcosx+2cos2x=
 sin2x+(1+cos2x)=2sin(2x+
sin2x+(1+cos2x)=2sin(2x+ )+1
)+1∴f(x)的最小正周期T=
 =π;
=π;(2)∵
 时,2x+
时,2x+ ∈
∈
∴当x=
 或
或 时,函数有最小值0;当x=
时,函数有最小值0;当x= 时,函数有最大值为3
时,函数有最大值为3当
 时,f(x)的值域的值域为[0,3].
时,f(x)的值域的值域为[0,3].点评:本题给出向量含有三函数的坐标,求函数的周期与值域.着重考查了向量的数量积、三角恒等变换公式和三角函数的图象与性质等知识,属于中档题.

练习册系列答案
相关题目
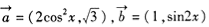
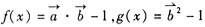
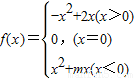


 ,函数
,函数
 时,求函数f(x)的值域.
时,求函数f(x)的值域.