题目内容
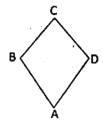
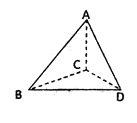
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,侧棱
,侧棱![]() 面
面![]() ,
,![]() .
.
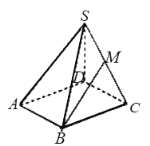
(1)若![]() 是
是![]() 的中点,求
的中点,求![]() 与
与![]() 所成的角;
所成的角;
(2)设![]() 是
是![]() 上一点,过
上一点,过![]() 的平面将四棱柱
的平面将四棱柱![]() 分成体积相等的两部分,求
分成体积相等的两部分,求![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)设菱形![]() 的边长为单位1,则
的边长为单位1,则![]() .取
.取![]() 的中点
的中点![]() ,连接
,连接![]() .可得
.可得![]() (或其补角)就是
(或其补角)就是![]() 与
与![]() 所成的角.在
所成的角.在![]() 中求出这个角即可;
中求出这个角即可;
(2)作出过![]() 的平面与侧面
的平面与侧面![]() 的交线为
的交线为![]() .可证得
.可证得![]() ,设
,设![]() ,
,![]() ,多面体
,多面体![]() 的体积等于三棱锥
的体积等于三棱锥![]() 与四棱锥
与四棱锥![]() 的体积之和,由此求得
的体积之和,由此求得![]() ,可得
,可得![]() .
.
设菱形![]() 的边长为单位1,则
的边长为单位1,则![]() .
.
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
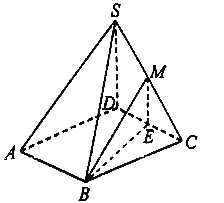
∵![]() 是
是![]() 是中点,∴
是中点,∴![]() ,
,![]() ,
,![]() ,
,![]() (或其补角)就是
(或其补角)就是![]() 与
与![]() 所成的角.
所成的角.
∵![]() 面
面![]() ,∴
,∴![]() 面
面![]() ,而
,而![]() 面
面![]() ,∴
,∴![]() .
.
在![]() 中,因为
中,因为![]() ,
,![]() ,
,
所以![]() ,即
,即![]() .
.
从而在![]() 中,
中,![]() ,故
,故![]() .
.
∴异面直线![]() 与
与![]() 所成的角的60°.
所成的角的60°.
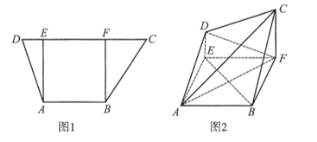
(2)如图,设过![]() 的平面与侧面
的平面与侧面![]() 的交线为
的交线为![]() .
.
∵![]() ,
,![]() 不在平面
不在平面![]() 内,∴
内,∴![]() 面
面![]() ,∴
,∴![]() ,于是
,于是![]() .
.
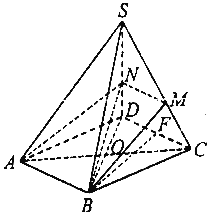
连接![]() ,
,![]() ,
,![]() ,设
,设![]() ,
,![]() ,
,
则直角梯形![]() 中,
中,![]() ,其面积
,其面积![]() .
.
过![]() 在平面
在平面![]() 内作
内作![]() ,
,![]() 是垂足,在等边三角形
是垂足,在等边三角形![]() 中,
中,![]() .
.
∵![]() 面
面![]() ,∴
,∴![]() ,得
,得![]() 面
面![]() ,
,
多面体![]() 的体积
的体积![]()
![]()
![]() ,
,
∴![]() ,
,![]() (舍去大于1的).
(舍去大于1的).
由![]() ,得
,得![]() .
.

【题目】某公司生产的某种产品,如果年返修率不超过千分之一,则其生产部门当年考核优秀,现获得该公司2011-2018年的相关数据如下表所示:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年生产台数(万台) | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 |
该产品的年利润(百万元) | 2.1 | 2.75 | 3.5 | 3.25 | 3 | 4.9 | 6 | 6.5 |
年返修台数(台) | 21 | 22 | 28 | 65 | 80 | 65 | 84 | 88 |
部分计算结果:
| ||||||||
注:年返修率=![]()
(1)从该公司2011-2018年的相关数据中任意选取3年的数据,以![]() 表示3年中生产部门获得考核优秀的次数,求
表示3年中生产部门获得考核优秀的次数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)根据散点图发现2015年数据偏差较大,如果去掉该年的数据,试用剩下的数据求出年利润![]() (百万元)关于年生产台数
(百万元)关于年生产台数![]() (万台)的线性回归方程(精确到0.01).
(万台)的线性回归方程(精确到0.01).
附:线性回归方程![]() 中,
中,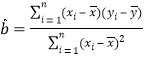
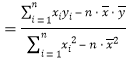 ,
,![]() .
.