Question

函数f(x)=x³-3tx+m(x∈R,m和t为实常数)是奇函数．

(1)求实数m的值和函数f(x)的图像与横轴的交点坐标；

(2)设g(x)=|f(x)|(x∈)，求g(x)的最大值F(t)；

(3)求F(t)的最小值．

Answer 1

解：(1)由于f(x)为奇函数，易得m=0 

设f(x)=x³=-3tx=x(x²-3t)=0

①当3t＜0时，上述方程只有一个实数根x=0,所以f(x)与x轴的交点坐标为(0,0)

②当3t=0时，上述方程有三个相等实数根x=0,所以f(x)与x轴的交点坐标为(0,0)

③当3t＞0时，上述方程的解为x₁=0,x_2,3=±t,所以f(x)与横轴的交点坐标分别为：(0,0),(t,0),(-t,0)

(2)显然g(x)=|x³-3tx|（x∈[-1,1]）是偶函数，所以只要求出g(x)=|x³-3xt|(x∈[0,1])的最大值即可.又(x)=3(x²-t)

①t≤0时，则在[0,1]上f(x)为增函数,∴f(x)≥f(0)=0

∴f(x)=g(x),故F(t)=f(1)=1-3t  （6分）

②t＞0时，则在[0,1]上(x)=3(x+)(x-)

(i)≥1即t≥1时，则在[0,1]上f(x)为减函数

∴f(x)≤f(0)=0,∴g(x)=-f(x),

故F(t)=-f(1)=3t-1  （8分）

(ii)0＜t＜1时，则在[0,1]上(x)=3(x+)(x-)

x	0	(0,)		(,1)	1
(x)		-	-	+
F(x)	0	↓	极小值-2t	↑	1-3t

所以可以画出g(x)的草图如下，并且由图可知：

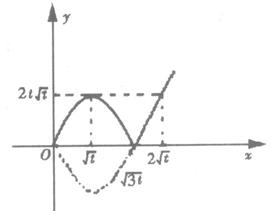
(1 )当＜1≤2即≤t＜1时，

g(x)最大值F(t)=-f()=2t

(2 )当1＞2即0＜t＜时，

g(x)的最大值F(t)=f(1)=1-3t 

综上所述：F(t)=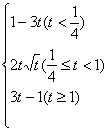 

(3)显然F（t）在（-∞，）上为减函数，

在上为增函数,

即在为增函数

∴F(t)的最小值=F.