题目内容
从直线L：y=x-2上一点P向圆C：x2+y2+2x-4y=0引切线，则切线长的最小值为
．
| ||
| 2 |
| ||
| 2 |
分析：把圆的方程化为标准方程，找出圆心坐标和圆的半径，要使切线长的最小，则必须点C到直线的距离最小．利用点到直线的距离公式求出圆心到直线y=x-2的距离即为|PC|的长，然后根据半径r，PC，PM满足勾股定理即可求出此时的切线长
解答：
解：圆的方程化为标准方程得（x+1）2+（y-2）2=5，
所以圆心C（-1，2），半径r=
，
要使切线长的最小，则必须点C到直线的距离最小．
过圆心C作垂直于直线y=x-2的直线，垂足为P时，满足题意
此时，圆心C（-1，2）到直线y=x-2的距离d=
∴所求的最小PM=
=
故答案为：
解：圆的方程化为标准方程得（x+1）2+（y-2）2=5，所以圆心C（-1，2），半径r=
| 5 |
要使切线长的最小，则必须点C到直线的距离最小．
过圆心C作垂直于直线y=x-2的直线，垂足为P时，满足题意
此时，圆心C（-1，2）到直线y=x-2的距离d=
| 5 | ||
|
∴所求的最小PM=
|
| ||
| 2 |
故答案为：
| ||
| 2 |
点评：本题的考点是直线与圆的位置关系，考查学生灵活运用点到直线的距离公式化简求值，解题的关键是找出切线长最短时的条件，根据题意画出相应的图形
练习册系列答案
相关题目
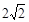个单位沿射线OM方向运动，设运动时间为t秒.问：当t为何值时直线PQ与圆C1相切？
．求y≥-x+b的概率．