题目内容

用数学归纳法证明

证明：(1)当n=1时,左边=,右边=,等式成立.

(2)假设n=k时,

当n=k+1时,

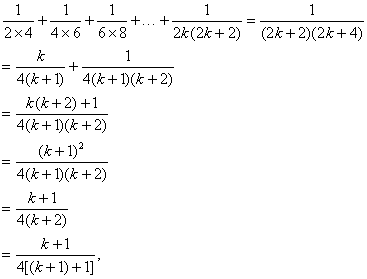
∴n=k+1时,等式成立.

由(1)(2),可得对一切正整数n∈N*等式都成立.

绿色通道:

在步骤(2)的证明过程中,突出了两个“凑”字，一“凑”假设,二“凑”结论,关键是要明确n=k+1时的证明目标,充分考虑由n=k到n=k+1时,命题形式之间的区别与联系.

在证明n=k+1时,直接使用裂项相减法求和,即

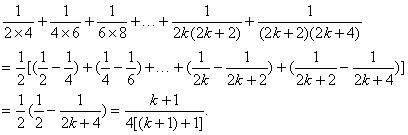
这里没有用归纳假设,是典型的套用数学归纳法的一种伪证.

练习册系列答案
相关题目
已知a＞0，b＞0，n＞1，n∈N*．用数学归纳法证明：
an+bn
2
≥(
a+b
2
)n．
已知m，n为正整数．
（Ⅰ）用数学归纳法证明：当x＞-1时，（1+x）m≥1+mx；
（Ⅱ）对于n≥6，已知(1-
1
n+3
)n＜
1
2
，求证(1-
m
n+3
)n＜(
1
2
)m，m=1，2…，n；
（Ⅲ）求出满足等式3n+4n+5n+…+（n+2）n=（n+3）n的所有正整数n．
用数学归纳法证明贝努利（Bernoulli）不等式：如果x是实数，且x＞-1，x≠0，n为大于1的自然数，那么有（1+x）n＞1+nx．
已知：函数f(x)=-
1
6
x3+
1
2
x2+x，x∈R．
（Ⅰ）求证：函数f（x）的图象关于点A(1，
4
3
)中心对称，并求f（-2007）+f（-2006）+…+f（0）+f（1）+…+f（2009）的值．
（Ⅱ）设g（x）=f′（x），an+1=g（an），n∈N+，且1＜a1＜2，求证：
（ⅰ）请用数学归纳法证明：当n≥2时，1＜an＜
3
2
；
（ⅱ）|a1-
2
|+|a2-
2
|+…+|an-
2
|＜2．
用数学归纳法证明：（cosα+isinα）n=cosnα+isinnα，（其中i为虚数单位）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网