题目内容
已知双曲线与椭圆可| x2 |
| 9 |
| y2 |
| 25 |
| 14 |
| 5 |
分析:先根据椭圆方程求得椭圆的焦点和离心率,进而根据题意求得双曲线的焦点和离心率,进而求得双曲线方程得长轴和短轴,则双曲线方程可得.
解答:解:依题意可知椭圆方程中a=5,b=3,
∴c=
=4
∴椭圆焦点为F(O,±4),离心率为e=
所以双曲线的焦点为F(O,±4),离心率为2,
从而双曲线中
求得c=4,a=2,b=2
.
所以所求双曲线方程为
-
=1
∴c=
| 25-9 |
∴椭圆焦点为F(O,±4),离心率为e=
| 4 |
| 5 |
所以双曲线的焦点为F(O,±4),离心率为2,
从而双曲线中
|
求得c=4,a=2,b=2
| 3 |
所以所求双曲线方程为
| y2 |
| 4 |
| x2 |
| 12 |
点评:本题主要考查了双曲线的标准方程和圆锥曲线的共同特征.考查了学生对圆锥曲线的综合理解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
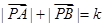 ,则动点P的轨迹为椭圆;
,则动点P的轨迹为椭圆;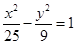 与椭圆
与椭圆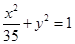 有相同的焦点;
有相同的焦点;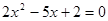 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;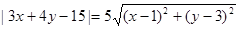 ,则点P的轨迹是一条直线.
,则点P的轨迹是一条直线.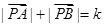 ,则动点P的轨迹为椭圆;
,则动点P的轨迹为椭圆;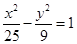 与椭圆
与椭圆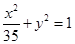 有相同的焦点;
有相同的焦点;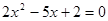 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;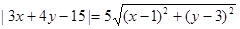 ,则点P的轨迹是一条直线.
,则点P的轨迹是一条直线. 与椭圆
与椭圆 有共同的准线;
有共同的准线;