题目内容
若点A(2,-3)是直线a1x+b1y+1=0和a2x+b2y+1=0的公共点,则相异的两点(a1,b1)和(a2,b2)所确定的直线方程是( )A.2x-3y+1=0 B.3x-2y+1=0
C.2x-3y-1=0 D.3x-2y-1=0
答案:A
解析:∵点A(2,-3)是直线a1x+b1y+1=0和a2x+b2y+1=0的公共点,
∴2a1-3b1+1=0,2a2-3b2+1=0.
两式相减,化简得![]() .
.
于是过相异两点(a1,b1),(a2,b2)的直线方程是y-b2=![]() (x-a2),即2x-3y-(2a2-3b2)=0.
(x-a2),即2x-3y-(2a2-3b2)=0.
又∵2a2-3b2+1=0,∴2a2-3b2=-1.
∴2x-3y+1=0.

练习册系列答案
相关题目
 过点P(1,1)且与线段AB相交,则直线
过点P(1,1)且与线段AB相交,则直线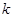 的取值范围是( )
的取值范围是( )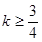 B.
B.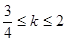 C.
C.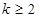 或
或 D.
D.