题目内容
(本小题满分12分)已知数列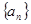 的首项为
的首项为 ,前
,前 项和为
项和为 ,且
,且
(1)求证:数列 成等比数列;
成等比数列;
(2)令 ,求函数
,求函数 在点
在点 处的导数
处的导数 .
.
【答案】
(1)证明略;
(2)

【解析】由已知 ,可得
,可得 两式相减得
两式相减得
 即
即 ……………………………2分
……………………………2分
从而 ………………………………….4分
………………………………….4分
当 时
时 所以
所以 又
又 所以
所以
从而
故总有 ,
, 又
又
从而 即数列
即数列 是等比数列;…………………………………5分
是等比数列;…………………………………5分
(II)由(I)知 ………………………………7分
………………………………7分
因为 所以
所以
从而 =
=
= -
- ……………………………9分
……………………………9分
= ………………………………12分
………………………………12分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
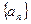 的首项为
的首项为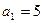 ,前
,前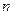 项和为
项和为 ,且
,且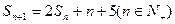
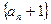 成等比数列;
成等比数列;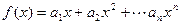 ,求函数
,求函数 在点
在点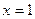 处的导数
处的导数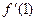 .
. 的各项都为正数,其前
的各项都为正数,其前 项和为
项和为 ,已知对任意
,已知对任意 ,
, 是
是 和
和 的等比中项.
的等比中项. 的通项公式;
的通项公式; ;
; ,
, ,且
,且 ,若存在
,若存在 ∈
∈ ,使对满足
,使对满足 的一切正整数
的一切正整数 恒成立,求这样的正整数
恒成立,求这样的正整数 的各项都为正数,其前
的各项都为正数,其前 项和为
项和为 ,已知对任意
,已知对任意 ,
, 是
是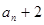 和
和 的等比中项.
的等比中项. 的通项公式;
的通项公式; ;
; ,
, ,且
,且 ,若存在
,若存在 ∈
∈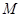 ,使对满足
,使对满足 的一切正整数
的一切正整数 恒成立,求这样的正整数
恒成立,求这样的正整数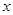 公里.经预算,修建一个轻轨中间站的费用为2000万元,修建
公里.经预算,修建一个轻轨中间站的费用为2000万元,修建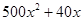 )万元.设余下工程的总费用为
)万元.设余下工程的总费用为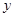 万元.
万元.