题目内容
如图，正四棱柱ABCD－A1B1C1D1中，AA1＝2AB＝4，点E在CC1上且C1E＝3EC．
(Ⅰ)证明：A1C⊥平面BED；
(Ⅱ)求二面角A1－DE－B的大小．
答案：
解析：
解析：
|
解法一：依题设知AB＝2，CE＝1． (Ⅰ)连结AC交BD于点F，则BD⊥AC．
由三垂线定理知，BD⊥A1C．在平面A1CA内，连结EF交A1C于点G， A1C与平面BED内两条相交直线BD，EF都垂直，所以A1C⊥平面BED． (Ⅱ)作GH⊥DE，垂足为H，连结A1H．由三垂线定理知A1H⊥DE， 故∠A1HG是二面角A1－DE－B的平面角． 解法二： 以D为坐标原点，射线DA为x轴的正半轴， 建立如图所示直角坐标系D－xyz．
|
练习册系列答案
相关题目
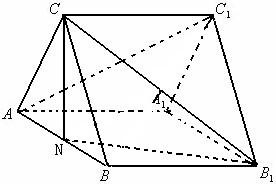如图是正三棱柱ABC-A1B1C1，AA1=3，AB=2，若N为棱AB中点．
如图是正三棱柱ABC-A1B1C1，AA1=3，AB=2，若N为棱AB中点．
