题目内容
已知：an=2n-1 则10a1+9a2+8a3+…+3a8+2a9+a10= ．
【答案】分析：设出S=10a1+9a2+8a3+…+3a8+2a9+a10，利用错位相减法求出S即可．
解答：解：设S=10a1+9a2+8a3+…+3a8+2a9+a10，
即S=10×2+9×21+8×22+…+3×27+2×28+29，…①，
①×2得2S=10×21+9×22+8×23+…+3×28+2×29+210，…②，
②-①得：S=-10×2+21+22+…+27+28+29+210
=2×
=211-12=2036，
故答案为：2036．
点评：本题考查数列求和的基本方法，考查错位相减法的应用，考查计算能力．
解答：解：设S=10a1+9a2+8a3+…+3a8+2a9+a10，
即S=10×2+9×21+8×22+…+3×27+2×28+29，…①，
①×2得2S=10×21+9×22+8×23+…+3×28+2×29+210，…②，
②-①得：S=-10×2+21+22+…+27+28+29+210
=2×
=211-12=2036，故答案为：2036．
点评：本题考查数列求和的基本方法，考查错位相减法的应用，考查计算能力．
练习册系列答案
相关题目
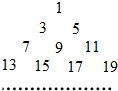（2011•潍坊二模）已知数列an=2n-1（n∈N*），把数列{an}的各项排成如图所示的三角形数阵，记（m，n）表示该数阵中第m行中从左到右的第n个数，则S（10，6）对应于数阵中的数是