Question

如图所示，三棱锥D—ABC中，DB⊥平面ABC，∠DAB=30°,∠BAC=45°,∠ACB=90°,BC=a,求：?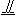

（1）AB与CD所成的角；?

（2）AB与CD间的距离.

Answer 1

解析：过C作CE⊥AB于E，则E是AB的中点，过E作EF BD，连结DF、CF，则BEFD为矩形.（∵DB⊥面ABC，∴DB⊥BC）?

（1）∵DF∥AB，∴∠CDF为AB与CD所成的角或其补角.?

∵BE⊥CE，BE⊥EF，且CE∩EF=E，?

∴BE⊥平面CEF.?

∴DF⊥平面CEF.∴DF⊥CF.?

∵BD⊥平面ABC，∴BD⊥BC.?

在Rt△ABC中，AB=,?

∴DF=BE=AB=a.?

在Rt△ADB中，BD=ABtan∠DAB=a·tan30°=.?

在Rt△CBD中，CD=.?

在Rt△CDF中，cos∠CDF=,?

∴∠CDF =arccos.因此AB与CD所成的角为arccos.?

（2）∵AB∥DF,AB平面CDF，?

∴AB∥平面CDF.?

?∴AB与CD的距离等于AB与平面CDF的距离，过E作EG⊥CF于G.?

∵DF⊥平面CEF，∴平面CEF⊥平面CDF.?

又EG⊥CF，平面CEF∩平面CDF=CF，∴EG⊥平面CDF，线段EG的长即为所求.?

∵EF∥BD，BD⊥平面ABC，∴EF⊥平面ABC，即EF⊥CE.?

在Rt△CEF中，CE=AB=a,EF=BD=a,?

∴EG=?

=.?

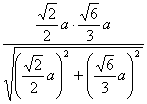∴AB与CD间的距离为a.