题目内容
已知点A(-3,0)和圆O:x2+y2=9,AB是圆O的直径,M和N是AB的三等分点,P(异于A,B)是圆O上的动点,PD⊥AB于D, ,直线PA与BE交于C,则当λ=________时,|CM|+|CN|为定值.
,直线PA与BE交于C,则当λ=________时,|CM|+|CN|为定值.

分析:设点P(x0,y0),则点E(x0,
 ),用点斜式求出PA、BE的方程,联立方程组求得点C满足的关系式,为
),用点斜式求出PA、BE的方程,联立方程组求得点C满足的关系式,为  +
+ =1,故点C在以AB为长轴的椭圆上,当M、N为此椭圆的焦点时,|CM|+|CN|为定值2a=6.再根据 a2-b2=c2 可得λ的值.
=1,故点C在以AB为长轴的椭圆上,当M、N为此椭圆的焦点时,|CM|+|CN|为定值2a=6.再根据 a2-b2=c2 可得λ的值.解答:由题意可得B(3,0),M(-1,0)、N(1,0),设点P(x0,y0),则点E(x0,
 ).
).故PA的方程为 y=
 •(x+3)…①,BE的方程为 y=
•(x+3)…①,BE的方程为 y= (x-3)…②.
(x-3)…②.由①②联立方程组可得 y2=
 (x-9).
(x-9).把
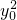 =9-
=9- 代入化简可得
代入化简可得  +
+ =1,故点C在以AB为长轴的椭圆上,当M、N为此椭圆的焦点时,
=1,故点C在以AB为长轴的椭圆上,当M、N为此椭圆的焦点时,|CM|+|CN|为定值2a=6.
此时,a=3,c=1,b=
 ,由 a2-b2=c2 可得 9-
,由 a2-b2=c2 可得 9- =1,求得λ=
=1,求得λ= ,
,故答案为
 .
.点评:本题主要考查直线和圆的位置关系,椭圆的定义和简单性质的应用,求两条直线的交点坐标,属于中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
已知点A(3,0),B(-
,1),C(cosa,sina),O(0,0),若|
+
|=
,a∈(0,π),则
与
的夹角为( )
| 3 |
| OA |
| OC |
| 13 |
| OB |
| OC |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,已知点A(
如图,已知点A(